Spherical cap practice problems - page 2 of 3
Direction: Solve each problem carefully and show your solution in each item.Number of problems found: 43
- Pilot
 How high can the airplane's pilot see 0.001 of Earth's surface?
How high can the airplane's pilot see 0.001 of Earth's surface? - Spherical segment
 The spherical segment with height h=2 has a volume of V=225. Calculate the radius of the sphere which is cut in this segment.
The spherical segment with height h=2 has a volume of V=225. Calculate the radius of the sphere which is cut in this segment. - The cylindrical container
 The cylindrical container has a base area of 300 cm³ and a height of 10 cm. It is 90% filled with water. We gradually insert metal balls into the water, each with a volume of 20 cm³. After inserting, how many balls does water flow over the edge of the con
The cylindrical container has a base area of 300 cm³ and a height of 10 cm. It is 90% filled with water. We gradually insert metal balls into the water, each with a volume of 20 cm³. After inserting, how many balls does water flow over the edge of the con - Portioning ice cream
 How many scoops of ice cream can we make using a scoop in the shape of a spherical canopy with a radius of 2.5 cm and a height of 4 cm. We have a 2-liter ice cream tub available. When portioning, we will follow the exact measure.
How many scoops of ice cream can we make using a scoop in the shape of a spherical canopy with a radius of 2.5 cm and a height of 4 cm. We have a 2-liter ice cream tub available. When portioning, we will follow the exact measure. - Sphere cut
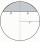 A sphere segment is cut off from a sphere k with radius r = 1. The volume of the sphere inscribed in this segment is equal to 1/6 of the segment's volume. What is the distance of the cutting plane from the center of the sphere?
A sphere segment is cut off from a sphere k with radius r = 1. The volume of the sphere inscribed in this segment is equal to 1/6 of the segment's volume. What is the distance of the cutting plane from the center of the sphere? - Spherical 63214
 The gas tank consists of a 16m high cylinder with a diameter of 28m, which is closed at the top by a spherical canopy. The center of the spherical surface lies 4m below the bottom of the cylinder. Please calculate the spherical surface's radius and the ca
The gas tank consists of a 16m high cylinder with a diameter of 28m, which is closed at the top by a spherical canopy. The center of the spherical surface lies 4m below the bottom of the cylinder. Please calculate the spherical surface's radius and the ca - Spherical cap
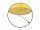 Place a part of the sphere on a 4.6 cm cylinder so that the surface of this section is 20 cm². Determine the radius r of the sphere from which we cut the spherical cap.
Place a part of the sphere on a 4.6 cm cylinder so that the surface of this section is 20 cm². Determine the radius r of the sphere from which we cut the spherical cap. - Spherical segment
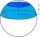 Calculate the volume of a spherical segment 18 cm high. The diameter of the lower base is 80 cm, and the upper base is 60 cm.
Calculate the volume of a spherical segment 18 cm high. The diameter of the lower base is 80 cm, and the upper base is 60 cm. - Spherical segment
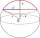 Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r = 5 cm and the radius of the circular base of the segment ρ = 4 cm.
Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r = 5 cm and the radius of the circular base of the segment ρ = 4 cm. - Sphere parts, segment
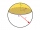 A sphere with a diameter of 20.6 cm, the cut is a circle with a diameter of 16.2 cm. What are the volume and surface of the segment?
A sphere with a diameter of 20.6 cm, the cut is a circle with a diameter of 16.2 cm. What are the volume and surface of the segment? - Stadium
 A domed stadium is shaped like a spherical segment with a base radius of 150 m. The dome must contain a volume of 3500000 m³. Determine the dome's height at its center to the nearest tenth of a meter.
A domed stadium is shaped like a spherical segment with a base radius of 150 m. The dome must contain a volume of 3500000 m³. Determine the dome's height at its center to the nearest tenth of a meter. - Sphere submerged in the cone
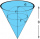 A right circular cone with a top width of 24 cm and an altitude of 8 cm is filled with water. A spherical steel ball with a radius of 3.0cm is submerged in the cone. Find the volume of water below the sphere.
A right circular cone with a top width of 24 cm and an altitude of 8 cm is filled with water. A spherical steel ball with a radius of 3.0cm is submerged in the cone. Find the volume of water below the sphere. - Spherical cap
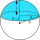 Calculate the volume of the spherical cap and the areas of the spherical canopy if r = 5 cm (radius of the sphere), ρ = 4 cm (radius of the circle of the cap).
Calculate the volume of the spherical cap and the areas of the spherical canopy if r = 5 cm (radius of the sphere), ρ = 4 cm (radius of the circle of the cap). - Spherical sector
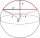 Calculate the volume and surface area of a spherical sector if the spherical segment that is part of the sector has a base radius r1 = 6 cm and a height v = 2 cm.
Calculate the volume and surface area of a spherical sector if the spherical segment that is part of the sector has a base radius r1 = 6 cm and a height v = 2 cm. - Hemisphere - roof
 The shape of the observatory dome is close to the hemisphere. Its outer diameter is 11 m. How many kilograms of paint and how many liters of thinner are used for its double coat if you know that 1 kg of paint diluted with 1 deciliter of thinner will paint
The shape of the observatory dome is close to the hemisphere. Its outer diameter is 11 m. How many kilograms of paint and how many liters of thinner are used for its double coat if you know that 1 kg of paint diluted with 1 deciliter of thinner will paint - The observatory
 The dome of the hemisphere-shaped observatory is 5.4 meters high. How many square meters of sheet metal need to be covered to cover it, and must we add 15 percent to the minimum amount due to joints and waste?
The dome of the hemisphere-shaped observatory is 5.4 meters high. How many square meters of sheet metal need to be covered to cover it, and must we add 15 percent to the minimum amount due to joints and waste? - Spherical bowl
 The bowl, in the shape of part of a spherical surface, has a diameter of 28 cm at the top edge and is 8 cm deep. What is the total volume of the bowl? How much water would you have to pour into the bowl to fill it halfway?
The bowl, in the shape of part of a spherical surface, has a diameter of 28 cm at the top edge and is 8 cm deep. What is the total volume of the bowl? How much water would you have to pour into the bowl to fill it halfway? - Two hemispheres
 In a wooden hemisphere with a radius r = 1, the carpenter created a hemispherical depression with a radius r/2. The bases of both hemispheres lie in the same plane. What is the surface of the created body (including the surface of the depression)?
In a wooden hemisphere with a radius r = 1, the carpenter created a hemispherical depression with a radius r/2. The bases of both hemispheres lie in the same plane. What is the surface of the created body (including the surface of the depression)? - The hemisphere
 The hemisphere container is filled with water. What is the radius of the container when 10 liters of water pour from it when tilted 30 degrees?
The hemisphere container is filled with water. What is the radius of the container when 10 liters of water pour from it when tilted 30 degrees? - Convex lens
 The convex lens consists of two spherical segments (dimensions given in mm). Calculate its weight if the density of the glass is 2.5 g/cm³. Dimensions: 60mm in length and width of the upper part 5mm, the width of the lower part 8mm
The convex lens consists of two spherical segments (dimensions given in mm). Calculate its weight if the density of the glass is 2.5 g/cm³. Dimensions: 60mm in length and width of the upper part 5mm, the width of the lower part 8mm
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
