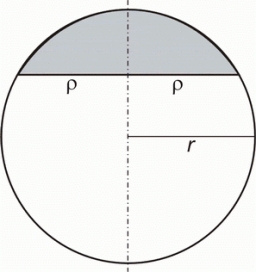
Sphere cut
A sphere segment is cut off from a sphere k with radius r = 1. The volume of the sphere inscribed in this segment is equal to 1/6 of the segment's volume. What is the distance of the cutting plane from the center of the sphere?
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
algebrasolid geometrybasic operations and conceptsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Sphere cuts
At what distance from the center does the sphere intersect with the radius R = 46 plane if the cut area and area of the main sphere circle are in ratio 2/5? - Cube corners
From the cube of edge 5 cm, we cut off all vertices so that each cutting plane intersects the edges 1 cm from the nearest vertice. How many edges will this body have? - Hemisphere layer
Find the volume of the spherical layer that results from a hemisphere with a radius of 5 cm by cutting a paragraph whose height is 1.5 cm. - A spherical segment
The aspherical section, whose axial section has an angle of j = 120° in the center of the sphere, is part of a sphere with a radius r = 10 cm. Calculate the cut surface. - Spherical 81527
Sketch a spherical layer formed from a sphere with a radius of r= 8.5cm, given: v=1.5cm, r1=7.7cm, r2=6.8cm. What is its volume? - Sphere from tree points
Equation of sphere with three-point (a,0,0), (0, a,0), (0,0, a) and center lies on plane x+y+z=a - Sphere
Intersect between the plane and a sphere is a circle with a radius of 60 mm. The cone, whose base is this circle and whose apex is at the center of the sphere, has a height of 34 mm. Calculate the surface area and volume of a sphere.
