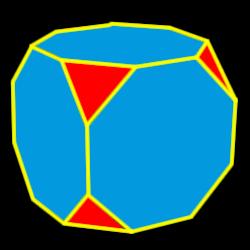
Cube corners
From the cube of edge 5 cm, we cut off all vertices so that each cutting plane intersects the edges 1 cm from the nearest vertice.
How many edges will this body have?
How many edges will this body have?
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Cube corners
We cut a small cube with an edge length of 2 cm from each corner of a large cube with an edge length of 10 cm. How many cm³ was the body left from the big cube after cutting the small cubes? - Opposite 79954
We color a wooden cube with an edge length of 3 cm so that three walls are blue, three are red, and no two opposite walls are the same color. Cut the cube into 1 cm³ cubes. How many cats will have at least one red wall and at least one blue wall? - Cutting the prism
A prism with a square base with an area of 1 cm² and a height of 3 cm was cut from a cube with an edge length of 3 cm. What is the body's surface formed from the cube after cutting the prism? - Sphere cut
A sphere segment is cut off from a sphere k with radius r = 1. The volume of the sphere inscribed in this segment is equal to 1/6 of the segment's volume. What is the distance of the cutting plane from the center of the sphere?
- Diagonals 3580
Cube edge length 5cm. Draw different diagonals. - Shortest walk
An ant is crawling around this cube. The cube is made of wire. Each side of the cube is 3 inches long. (Those sides are called edges.) Points A and B are vertices of the cube. What is the least distance the ant would have to crawl if it starts from point - Cutting circles
From the square 1 m sides, we have to cut the circles with a radius of 10 cm. How many discs will we cut, and how many percent will be wasted?
