Sphere
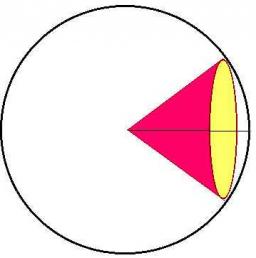
Intersect between the plane and a sphere is a circle with a radius of 60 mm. The cone, whose base is this circle and whose apex is at the center of the sphere, has a height of 34 mm. Calculate the surface area and volume of a sphere.
Your answer:
Your answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
The Pythagorean theorem is the base for the right triangle calculator.
The Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
arithmeticsolid geometryplanimetryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- A plane vs. sphere
The intersection of a plane is 2 cm from the sphere's center, and this sphere is a circle whose radius is 6 cm. Calculate the surface area and volume of the sphere. - Surface and volume
Calculate the surface and volume of a cylinder whose height is 8 dm and the radius of the base circle is 2 dm. - Cone measurements
Calculate the volume and surface of the rotating cone with the base radius r = 4.6 dm and the height v = 230 mm. - Cylinder - basics
A cylinder has a base radius r = 24 cm and height h = 62 cm. Calculate: a) The area of the base - Rotating cone
Calculate the volume and the surface area of a rotating cone of base radius r = 2.3 dm and a height h = 46 mm. - Sphere cuts
At what distance from the centre does a plane intersect a sphere of radius R = 46, if the area of the circular cross-section and the area of the great circle are in the ratio 2:5? - Calculate cone
The rotating cone has a base radius r = 226 mm, and the deviation of the side from the base plane is 56°. Calculate the height of the cone.
