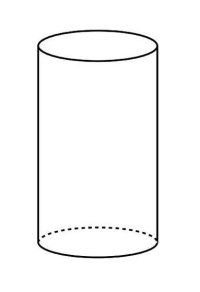
Cylinder - basics
Cylinder with base radius r = 54 cm and height h=35 cm. Calculate:
a) Area of the base
a) Area of the base
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Calculate 24011
There is a cylinder with a base radius of 3 cm and a height of 12 cm. Calculate a) cylinder surface b) cylinder volume - Calculate 24941 Calculate the surface and volume of a cylinder with a base radius of 5 cm and a height of 8 cm.
- Calculate 6635
Calculate the radius of the cylinder base if you know its volume V and height v. H = 300 cm3, h = 8 cm - Surface and volume
Calculate the surface and volume of a cylinder whose height is 8 dm and the radius of the base circle is 2 dm. - Cylinder surface area
The volume of a cylinder whose height is equal to the radius of the base is 678.5 dm³. Calculate its surface area. - Relationship 4417
Calculate the volume of the cylinder if the radius of the base is 3 cm, and the relationship between the radius of the base and the height of the cylinder is v = 3r - Cylinder
The cylinder surface is 922 dm². Its height is equal to the radius of the base. Calculate the height of this cylinder. - Shell of cylinder
Calculate the area of the shell of the 1.6 m height cylinder with a base radius of 0.4 m. - Axial section
The axial section of the cylinder has a diagonal 31 cm long, and we know that the area of the side and the base area is in ratio 3:2. Calculate the height and radius of the cylinder base. - Rotating cone
Calculate the volume of a rotating cone with base radius r=12 cm and height h=7 cm. - Calculate 3016
Calculate the height of the cylinder if you know its surface S and the radius of the base r. a) r = 2 cm, S = 120 cm square b) r = 7 dm, S = 4,000 dm square c) r = 0.2 m, S = 20 square meters - Rotating cone II Calculate the area of the surface of a rotating cone with base radius r=19 cm and height h=9 cm.
- Cylinder surface, volume
The area of the base and the area of the shell are in the ratio of 3:5. Its height is 5 cm less than the radius of the base. Calculate both surface area and volume. - Cylindrical container An open-topped cylindrical container has a volume of V = 3140 cm³. Find the cylinder dimensions (radius of base r, height v) so that the least material is needed to form the container.
- Cans
How many m² of metal sheet is needed to produce 20,000 cans in the shape of a cylinder with a base radius and a height of 5 cm? - Transporting 17193
A barrel for transporting fuel has a height of 90 cm and a radius of the base of 30 cm. How many square meters of sheet metal are needed to make a barrel? - Calculate 20893
The volume of the cylinder is 193 cm3, and the radius of its base is 6.4 cm. Calculate the height and surface of the cylinder to 1 decimal place.
