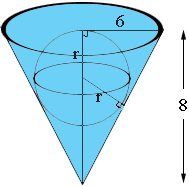
Sphere submerged in the cone
A right circular cone with a top width of 24 cm and an altitude of 8 cm is filled with water. A spherical steel ball with a radius of 3.0cm is submerged in the cone. Find the volume of water below the sphere.
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- solid geometry
- cone
- sphere
- body volume
- spherical cap
- planimetrics
- triangle
- goniometry and trigonometry
- sine
- cosine
- tangent
- arctangent
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Spherical 63214
The gas tank consists of a 16m high cylinder with a diameter of 28m, which is closed at the top by a spherical canopy. The center of the spherical surface lies 4m below the bottom of the cylinder. Please calculate the spherical surface's radius and the ca - The hemisphere
The hemisphere container is filled with water. What is the radius of the container when 10 liters of water pour from it when tilted 30 degrees? - Spherical tank
The water tower tank is a sphere with a radius of 35ft. If the tank is filled to one-quarter full, what is the height of the water? - Confectionery 7318
The confectioner needs to carve a cone-shaped decoration from a ball-shaped confectionery mass with a radius of 25 cm. Find the radius of the base of the ornament a (and the height h). He uses as much material as possible is used to make the ornament.
- A spherical segment
The aspherical section, whose axial section has an angle of j = 120° in the center of the sphere, is part of a sphere with a radius r = 10 cm. Calculate the cut surface. - Cylindrical 16713
Twenty identical steel balls were dropped into a cylindrical container of water standing on a horizontal surface to submerge them below the surface. At the same time, the water level rose by 4 mm. Determine the radius of one sphere if the diameter of the - Similar frustums
The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums?
