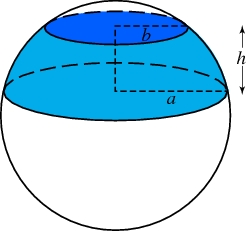
Spherical segment
Calculate the volume of a spherical segment 18 cm high. The diameter of the lower base is 80 cm, and the upper base is 60 cm.
Final Answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticsolid geometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Cone - bases
The volume of the cut cone is V = 38000π cm³. The radius of the lower base is 10 cm larger than the radius of the upper base. Determine the radius of the base if height v = 60 cm. - Convex lens
The convex lens consists of two spherical segments (dimensions given in mm). Calculate its weight if the density of the glass is 2.5 g/cm³. Dimensions: 60mm in length and width of the upper part 5mm, the width of the lower part 8mm - Spherical sector
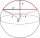Calculate the volume and surface area of a spherical sector if the spherical segment that is part of the sector has a base radius r1 = 6 cm and a height v = 2 cm. - Quadrilateral 21523
Calculate the surface area and volume of a regular quadrilateral pyramid if the edge of the lower base is 18 cm and the edge of the upper base is 15 cm. The wall height is 9 cm. - Frustum of a cone
A reservoir contains 28.54 m³ of water when complete. The diameter of the upper base is 3.5 m, while the lower base is 2.5 m. Find the height if the reservoir is in the form of a frustum of a right circular cone. - Truncated pyramid
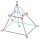The truncated regular quadrilateral pyramid has a volume of 74 cm3, a height v = 6 cm, and an area of the lower base 15 cm² greater than the upper base's area. Calculate the area of the upper base. - Spherical segment
Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r = 5 cm and the radius of the circular base of the segment ρ = 4 cm.
