Sphere in cone

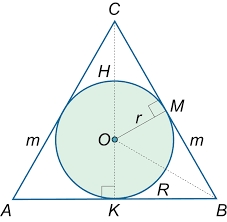
A sphere is inscribed in the cone (the intersection of their boundaries consists of a circle and one point). The ratio of the surface of the ball and the contents of the base is 4: 3. A plane passing through the axis of a cone cuts the cone in an isosceles triangle. Determine the size of the angle with respect to the base of this triangle.

Correct answer:

A =  60 °

Step-by-step explanation:

$$\begin{gathered} G=1 \\ G:S_1=4:3 \\ {S}_1={\displaystyle \frac{3}{4}}\cdot G={\displaystyle \frac{3}{4}}\cdot 1=0.75 \\ {S}_1=\pi r_1^2 \\ {r}_1=\sqrt{S_1\mathrm{/}\pi }=\sqrt{0.75\mathrm{/}3.1416}\doteq 0.4886 \\ G=4\pi r_2^2 \\ {r}_2=\sqrt{{\displaystyle \frac{G}{4\pi }}}=\sqrt{{\displaystyle \frac{1}{4\cdot 3.1416}}}\doteq 0.2821 \\ \tan \alpha =r_2:r_1 \\ \alpha =\arctan (r_2\mathrm{/}{r}_1)=\arctan (0.2821\mathrm{/}0.4886)\doteq 0.5236\text{ rad } \\ {\alpha }_2=2\cdot \alpha =2\cdot 0.5236\doteq 1.0472\text{ rad } \\ A={\alpha }_2{\to }^{\circ }={\alpha }_2\cdot {{\displaystyle \frac{180}{\pi }}}^{\circ }=1.0472\cdot {{\displaystyle \frac{180}{\pi }}}^{\circ }=60^{\circ }=60^{\circ } \end{gathered}$$

Try another example

Related math problems and questions:

• The cone
  The lateral surface area of the cone is 4 cm², the area of the base of the cone is 2 cm². Determine the angle in degrees (deviation) of the cone sine and the cone base plane. (Cone side is the segment joining the vertex cone with any point of the base c
• Glass
  How many glass are needed to produce glass with base regular 5-gon if one base triangle in the base is 4.2 square cm and the height is 10 cm?
• Angle of deviation
  The surface of the rotating cone is 30 cm² (with circle base), its surface area is 20 cm². Calculate the deviation of the side of this cone from the plane of the base.
• Pentadecagon
  Calculate the content of a regular 15-sides polygon inscribed in a circle with radius r = 4. Express the result to two decimal places.
• Ratio in trapezium
  The height v and the base a, c in the trapezoid ABCD are in the ratio 1: 6: 3, its content S = 324 square cm. Peak angle B = 35 degrees. Determine the perimeter of the trapezoid
• Isosceles triangle 10
  In an isosceles triangle, the equal sides are 2/3 of the length of the base. Determine the measure of the base angles.
• Lateral surface area
  The ratio of the area of the base of the rotary cone to its lateral surface area is 3: 5. Calculate the surface and volume of the cone, if its height v = 4 cm.
• Ratio iso triangle
  The ratio of the sides of an isosceles triangle is 7:6:7 Find the base angle to the nearest answer correct to 3 significant figure.
• Four sided prism
  Calculate the volume and surface area of a regular quadrangular prism whose height is 28.6cm and the body diagonal forms a 50-degree angle with the base plane.
• Cone A2V
  The surface of the cone in the plane is a circular arc with central angle of 126° and area 415 cm². Calculate the volume of a cone.
• Tetrahedral pyramid
  Determine the surface of a regular tetrahedral pyramid when its volume is V = 120 and the angle of the sidewall with the base plane is α = 42° 30'.
• Cone and the ratio
  The rotational cone has a height 43 cm, and the ratio of the base surface to lateral surface is 5: 7. Calculate the surface of the base and the lateral surface.
• Axial section of the cone
  The axial section of the cone is an isosceles triangle in which the ratio of cone diameter to cone side is 2: 3. Calculate its volume if you know its area is 314 cm square.
• Cone side
  Calculate the volume and area of the cone whose height is 10 cm and the axial section of the cone has an angle of 30 degrees between height and the cone side.
• Flowerbed
  Flowerbed has the shape of an isosceles obtuse triangle. Arm has a size 5.5 meters and an angle opposite to the base size is 94°. What is the distance from the base to opposite vertex?
• Cone
  Calculate volume and surface area of ​​the cone with a diameter of the base d=15 cm and side of the cone with the base has angle 52°.
• Base diagonal
  In a regular 4-sided pyramid, the side edge forms an angle of 55° with the base's diagonal. The length of the side edge is eight meters. Calculate the surface area and volume of the pyramid.