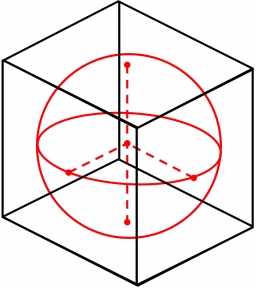
Inscribed circle
A circle is inscribed at the bottom wall of the cube with an edge (a = 1). What is the radius of the spherical surface that contains this circle and one of the vertex of the top cube base?
Final Answer:
Tips for related online calculators
The Pythagorean theorem is the base for the right triangle calculator.
See also our trigonometric triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetricsGrade of the word problem
Related math problems and questions:
- Spherical 63214
 The gas tank consists of a 16m high cylinder with a diameter of 28m, which is closed at the top by a spherical canopy. The center of the spherical surface lies 4m below the bottom of the cylinder. Please calculate the spherical surface's radius and the ca
The gas tank consists of a 16m high cylinder with a diameter of 28m, which is closed at the top by a spherical canopy. The center of the spherical surface lies 4m below the bottom of the cylinder. Please calculate the spherical surface's radius and the ca - RT - inscribed circle
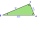 In a rectangular triangle with sides lengths> a = 30cm and b = 12.5cm, the right angle is at vertex C. Calculate the radius of the inscribed circle.
In a rectangular triangle with sides lengths> a = 30cm and b = 12.5cm, the right angle is at vertex C. Calculate the radius of the inscribed circle. - Inscribed circle
 XYZ is a right triangle with a right angle at the vertex X and an inscribed circle with a radius of 5 cm. Find the area of the triangle XYZ if XZ = 14 cm.
XYZ is a right triangle with a right angle at the vertex X and an inscribed circle with a radius of 5 cm. Find the area of the triangle XYZ if XZ = 14 cm. - 9-gon pyramid
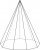 Calculate a nine-sided pyramid's volume and surface, the base of which can be inscribed with a circle with radius ρ = 7.2 cm and whose side edge s = 10.9 cm.
Calculate a nine-sided pyramid's volume and surface, the base of which can be inscribed with a circle with radius ρ = 7.2 cm and whose side edge s = 10.9 cm. - Sphere cut
 A sphere segment is cut off from a sphere k with radius r = 1. The volume of the sphere inscribed in this segment is equal to 1/6 of the segment's volume. What is the distance of the cutting plane from the center of the sphere?
A sphere segment is cut off from a sphere k with radius r = 1. The volume of the sphere inscribed in this segment is equal to 1/6 of the segment's volume. What is the distance of the cutting plane from the center of the sphere? - Pyramid in cube
 In a cube with an edge 12 dm long, we have an inscribed pyramid with the apex at the center of the cube's upper wall. Calculate the volume and surface area of the pyramid.
In a cube with an edge 12 dm long, we have an inscribed pyramid with the apex at the center of the cube's upper wall. Calculate the volume and surface area of the pyramid. - Billiard balls
 A layer of ivory billiard balls radius of 6.35 cm is in the form of a square. The balls are arranged so that each ball is tangent to everyone adjacent to it. In the spaces between sets of 4 adjacent balls, other balls rest, equal in size to the original.
A layer of ivory billiard balls radius of 6.35 cm is in the form of a square. The balls are arranged so that each ball is tangent to everyone adjacent to it. In the spaces between sets of 4 adjacent balls, other balls rest, equal in size to the original.
