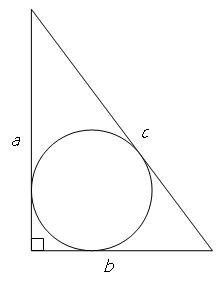
Inscribed circle
XYZ is a right triangle with a right angle at the vertex X and an inscribed circle with a radius of 5 cm. Find the area of the triangle XYZ if XZ = 14 cm.
Your answer:
Your answer:
Tips for related online calculators
See also our right triangle calculator.
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- RT - inscribed circle
In a rectangular triangle with sides lengths> a = 30 cm and b = 12.5 cm, the right angle is at vertex C. Calculate the radius of the inscribed circle. - Inscribed circle
A circle is inscribed at the bottom wall of the cube with an edge (a = 1). What is the radius of the spherical surface that contains this circle and one of the vertex of the top cube base? - Hexagon area calculation
Calculate the area of a regular hexagon inscribed in a circle with a radius r = 7 cm. - 30-gon
The radius of the inscribed circle is 15 cm at a regular 30-gon. Find the side length a, circle radius R, circumference, and area. - Drawing Similar Triangle
Isosceles triangle X'Y'Z' . It is similar to triangle XYZ. The base of triangle XYZ has length |XY|=4 cm. The size of the angle at the X vertex is 45 degrees. Draw a triangle X'Y'Z' whose base is 8 cm long. - Hexagon A
Calculate the area of a regular hexagon inscribed in a circle with radius r=15 cm. - Nonagon
Calculate the area and perimeter of a regular nonagon if its radius of the inscribed circle is r = 10 cm.
