RT - inscribed circle
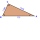
In a rectangular triangle with sides lengths> a = 30 cm and b = 12.5 cm, the right angle is at vertex C. Calculate the radius of the inscribed circle.
Final Answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
planimetryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Rectangular
Rectangular triangle KLM with right angle at vertex L, angle beta at vertex K, and angle alpha at vertex M. Angle at vertex M = 65°, side l = 17.5 cm. Use Pythagorean theorems and trigonometric functions to calculate the lengths of all sides and the angle - Inscribed circle
XYZ is a right triangle with a right angle at the vertex X and an inscribed circle with a radius of 5 cm. Find the area of the triangle XYZ if XZ = 14 cm. - Calculate ΔRST
In a right triangle RST with a right angle at the vertex T, we know the lengths of two sides: s = 7.8 cm and t = 13 cm; calculate the third side r. - Rhombus
A rhombus has a side length of a = 20 cm. The points where the inscribed circle touches the sides divide each side into segments of length a₁ = 13 cm and a₂ = 7 cm. Calculate the radius r of the inscribed circle and the lengths of the diagonals of the rho - Trapezoid RT
The plot is a rectangular trapezium ABCD, where ABIICD has a right angle at the vertex B side and AB has a length of 36 m. The lengths of the sides AB and BC are in the ratio 12:7. The lengths of the sides AB and CD are in the ratio 3:2. Calculate the con - Quadrilateral angle circle
The points ABC lie on the circle k(S, r) such that the angle at B is obtuse. How large must the angle at vertex B of quadrilateral SCBA be so that this angle is three times greater than the interior angle ASC of the same quadrilateral? - Triangle sides
Calculate the lengths of the sides of the triangle ABC, in which angles α = 113°, β = 48°, and the radius of the circle of the triangle described is r = 10 cm.
