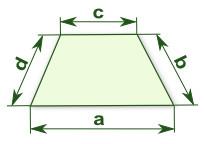
Trapezoid RT
The plot is a rectangular trapezium ABCD, where ABIICD has a right angle at the vertex B side and AB has a length of 36 m. The lengths of the sides AB and BC are in the ratio 12:7. The lengths of the sides AB and CD are in the ratio 3:2. Calculate the consumption mesh for the fence plot.
Correct answer:
Tips for related online calculators
Check out our ratio calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Rectangular trapezoid
The ABCD rectangular trapezoid with the AB and CD bases is divided by the diagonal AC into two equilateral rectangular triangles. The length of the diagonal AC is 62cm. Calculate the trapezium area in cm square and calculate how many different perimeters - Isosceles 37621
In the isosceles trapezoid ABCD, its bases AB = 20cm, CD = 12cm and arms AD = BC = 8cm are given. Specify its height and alpha angle at vertex A - Quadrilateral 80729
Quadrilateral ABCD has side lengths AB=13cm, CD=3cm, AD=4cm. Angles ACB and ADC are right angles. Calculate the perimeter of quadrilateral ABCD. - Calculate 82578
The vertices of triangle ABC are: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Calculate the lengths of sides AB, AC and the angle at vertex A.
- Trapezium ABCD
The figure shows ABDC is a trapezium in which AB || CD. Line segments RN and LM are drawn parallel to AB such that AJ=JK=KP. If AB=0.5m and AP=BQ=1.8m, find the lengths of AC, BD, RN, and LM. angle D=angle C=60 - Triangle ABC
There is the triangle ABC with the side BC of length 2 cm. Point K is the middle point of AB. Points L and M split the AC side into three equal lines. KLM is an isosceles triangle with a right angle at point K. Determine the lengths of the sides AB, AC tr - RT - inscribed circle
In a rectangular triangle with sides lengths> a = 30cm and b = 12.5cm, the right angle is at vertex C. Calculate the radius of the inscribed circle.
