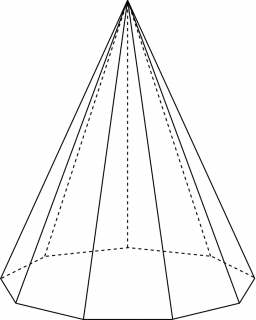
9-gon pyramid

Calculate the volume and the surface of a nine-sided pyramid, the base of which can be inscribed with a circle with radius ρ = 7.2 cm and whose side edge s = 10.9 cm.

Correct answer:

V =  409.0382 cm³
S =  299.899 cm²

Step-by-step explanation:

$$\begin{gathered} \rho =7.2\text{ cm } \\ s=10.9\text{ cm } \\ n=9 \\ {h}^2+{\rho }^2=s^2 \\ h=\sqrt{s^2-{\rho }^2}=\sqrt{10.9^2-7.2^2}\doteq 8.1835\text{ cm } \\ \alpha ={\displaystyle \frac{2\pi }{2\cdot n}}={\displaystyle \frac{2\cdot 3.1416}{2\cdot 9}}\doteq 0.3491\text{ rad } \\ \sin \alpha =a\mathrm{/}2:\rho \\ a=2\cdot \rho \cdot \sin (\alpha )=2\cdot 7.2\cdot \sin (0.3491)\doteq 4.9251\text{ cm } \\ {h}_2=\sqrt{{\rho }^2-(a\mathrm{/}2{)}^2}=\sqrt{7.2^2-(4.9251\mathrm{/}2{)}^2}\doteq 6.7658\text{ cm } \\ {S}_1={\displaystyle \frac{a\cdot h_2}{2}}={\displaystyle \frac{4.9251\cdot 6.7658}{2}}\doteq 16.6611\text{ cm } \\ {S}_9=n\cdot S_1=9\cdot 16.6611\doteq 149.9495{\text{cm}}^2 \\ V={\displaystyle \frac{1}{3}}\cdot S_9\cdot h={\displaystyle \frac{1}{3}}\cdot 149.9495\cdot 8.1835=409.0382{\text{cm}}^3 \end{gathered}$$

$$\begin{gathered} S_2={\displaystyle \frac{a\cdot h_2}{2}}={\displaystyle \frac{4.9251\cdot 10.6182}{2}}\doteq 16.6611{\text{cm}}^2 \\ {h}_2=\sqrt{h^2+h_2^2}=\sqrt{8.1835^2+10.6182^2}\doteq 10.6182\text{ cm } \\ S=S_9+n\cdot S_2=149.9495+9\cdot 16.6611=299.899{\text{cm}}^2 \end{gathered}$$

Try another example

Related math problems and questions:

• Hexagonal pyramid
  Calculate the surface area of a regular hexagonal pyramid with a base inscribed in a circle with a radius of 8 cm and a height of 20 cm.
• Hexagonal pyramid
  Find the volume of a regular hexagonal pyramid, the base edge of which is 12 cm long and the side edge 20 cm.
• Quadrilateral pyramid
  Calculate the surface of a quadrilateral pyramid, which has a rectangular base with dimensions a = 8 cm, b = 6 cm and height H = 10 cm.
• Hexagonal pyramid
  Calculate the volume and the surface of a regular hexagonal pyramid with a base edge length of 3 cm and a height of 5 cm.
• Tetrahedral pyramid
  A regular tetrahedral pyramid is given. Base edge length a = 6.5 cm, side edge s = 7.5 cm. Calculate the volume and the area of its face (side area).
• Quadrilateral pyramid
  We have a regular quadrilateral pyramid with a base edge a = 10 cm and a height v = 7 cm. Calculate 1/base content 2/casing content 3/pyramid surface 4/volume of the pyramid
• Hexagonal pyramid
  The base of the pyramid is a regular hexagon, which can be circumscribed in a circle with a radius of 1 meter. Calculate the volume of a pyramid 2.5 meters high.
• Pentagonal pyramid
  The height of a regular pentagonal pyramid is as long as the edge of the base, 20 cm. Calculate the volume and surface area of the pyramid.
• Hexagon cut pyramid
  Calculate the volume of a regular 6-sided cut pyramid if the bottom edge is 30 cm, the top edge is 12 cm, and the side edge length is 41 cm.
• Quadrilateral pyramid,
  A quadrilateral pyramid, which has a rectangular base with dimensions of 24 cm, 13 cm. The height of the pyramid is 18cm. Calculate 1/the area of the base 2/casing area 3/pyramid surface 4/volume of the pyramid
• Base diagonal
  In a regular 4-sided pyramid, the side edge forms an angle of 55° with the base's diagonal. The length of the side edge is eight meters. Calculate the surface area and volume of the pyramid.
• Quadrangular pyramid
  The regular quadrangular pyramid has a base length of 6 cm and a side edge length of 9 centimeters. Calculate its volume and surface area.
• Triangular pyramid
  Calculate the volume and surface area of a regular triangular pyramid with height equal to the base edge 10 cm length.
• Pyramid
  The pyramid has a base rectangle with a = 6cm, b = 8cm. The side edges are the same, and their length = 12.5 cm. Calculate the surface of the pyramid.
• The pyramid 4s
  The pyramid with a rectangular base measuring 6 dm and 8 dm has a side edge of length 13 dm. Calculate the surface area and volume of this pyramid.
• Pyramid 8
  Calculate the volume and the surface area of a regular quadrangular pyramid with the base side 9 cm and side wall with the base has an angle 75°.
• Hexagonal pyramid
  Calculate the volume and surface area of a regular hexagonal pyramid with a base edge a = 30 m and a side edge b = 50 m.