Koule ve kuželi
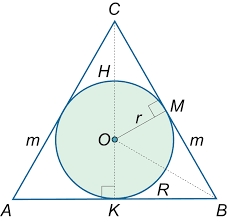
Do kužele je vepsána koule (průnik jejich hranic se skládá z kružnice a jednoho bodu). Poměr povrchu koule a obsahu podstavy je 4: 3. Rovina, která prochází osou kužele, řeže kužel v rovnoramenném trojúhelníku. Určete velikost úhlu oproti základně tohoto trojúhelníku.
Vaše odpověď:
Vaše odpověď:
Zobrazuji 1 komentář:
Žák
Správně G : S = 4 : 3 => S = 3/4*G => r1 = r2*sqrt(3). Úhel alfa2 = 60 stupňů. Uvedený postup výpočtu velikosti úhlu lze použít výhradně pro zadaný poměr 4 : 3, kdy rovina řeže kužel v rovnostranném trojúhelníku.
Tipy na související online kalkulačky
Vyzkoušejte naši kalkulačka na přepočet poměru.
Chcete proměnit jednotku plochy?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Chcete proměnit jednotku plochy?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
