Examples for secondary school students - page 118 of 231
Number of problems found: 4608
- Profit growth
 A company's profit increased by 25% during 1992, increased by 40% during 1993, decreased by 20% in 1994, and increased by 10% during 1995. Find the average growth in the profit level over the four years.
A company's profit increased by 25% during 1992, increased by 40% during 1993, decreased by 20% in 1994, and increased by 10% during 1995. Find the average growth in the profit level over the four years. - Isosceles triangle 8
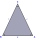 If the rate of the sides of an isosceles triangle is 7:6:7, find the base angle correct to the nearest degree.
If the rate of the sides of an isosceles triangle is 7:6:7, find the base angle correct to the nearest degree. - Carpenters
 Carpenters 1 and 2 spend ten days and five days, respectively, to make one table. The first carpenter and 30 made 50 tables by the second. What is the average time spent on the products?
Carpenters 1 and 2 spend ten days and five days, respectively, to make one table. The first carpenter and 30 made 50 tables by the second. What is the average time spent on the products? - Children 8088
 There are men, women, and children in society. There are 3 times more men than women and 5 more children than women. If 6 more men and 6 women came, men would be half the company. How many women, men, and children are there?
There are men, women, and children in society. There are 3 times more men than women and 5 more children than women. If 6 more men and 6 women came, men would be half the company. How many women, men, and children are there? - Cable car
 Find the elevation difference of the cable car when it rises by 67 per mille, and the rope length is 930 m.
Find the elevation difference of the cable car when it rises by 67 per mille, and the rope length is 930 m. - Incorrectly 8075
 Katka solved an example from mathematics. She could calculate 50% of the examples, guess the remaining questions, and guess one-fifth of them. She had 12 answers incorrectly. How many tasks did the test contain?
Katka solved an example from mathematics. She could calculate 50% of the examples, guess the remaining questions, and guess one-fifth of them. She had 12 answers incorrectly. How many tasks did the test contain? - Prospering students
 There are 30 girls and 30 boys in the class. Boys are prospering 28, girls all. If all the prospering students are 95%, how many girls are in the class and how many boys are there?
There are 30 girls and 30 boys in the class. Boys are prospering 28, girls all. If all the prospering students are 95%, how many girls are in the class and how many boys are there? - Spherical cap 4
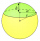 What is the surface area of a spherical cap, the base diameter of 20 m, and the height of 2.5 m? Calculate using the formula.
What is the surface area of a spherical cap, the base diameter of 20 m, and the height of 2.5 m? Calculate using the formula. - Employees 8068
 One thousand employees work in the company. At the end of the year, 10% of all men and 20% of all women received bonuses. Thus, the company rewarded 14% of the total number of employees. How many men and women work in the company?
One thousand employees work in the company. At the end of the year, 10% of all men and 20% of all women received bonuses. Thus, the company rewarded 14% of the total number of employees. How many men and women work in the company? - Power input
 The construction lift lifted a 300 kg load to a height of 12 m with uniform movement. If the efficiency is 75% and the engine has a power input of 5 kW, how long did it take for the load to be lifted?
The construction lift lifted a 300 kg load to a height of 12 m with uniform movement. If the efficiency is 75% and the engine has a power input of 5 kW, how long did it take for the load to be lifted? - A screen
 A screen is 1680 x 1050 pixels. What are the coordinates (and size in pixels) of a central area which is exactly 33% of the screen size?
A screen is 1680 x 1050 pixels. What are the coordinates (and size in pixels) of a central area which is exactly 33% of the screen size? - Three-digit integers
 How many three-digit natural numbers exist that do not contain zero and are divisible by five?
How many three-digit natural numbers exist that do not contain zero and are divisible by five? - Kilograms of sugar
 When weighing twenty-kilogram bags of sugar, we found the following values in kg: 1.00; 1.01; 1.05; 0.99; 1.00; 0.98; 0.99; 1.04; 1.06; 0.93; 1.00; 1.03; 0.97; 1.00; 0.99; 1.05; 1.01; 0.94; 1.00 Compile the honesty table to find the mean, mode, and median
When weighing twenty-kilogram bags of sugar, we found the following values in kg: 1.00; 1.01; 1.05; 0.99; 1.00; 0.98; 0.99; 1.04; 1.06; 0.93; 1.00; 1.03; 0.97; 1.00; 0.99; 1.05; 1.01; 0.94; 1.00 Compile the honesty table to find the mean, mode, and median - Represented 8020
 The race was divided into four stages. The length of Stages 1 and 4 was 160 km. The length of the second stage represented a third of the total length of the race. The length of the 4th stage was twice as long as the third stage. What percentage of the to
The race was divided into four stages. The length of Stages 1 and 4 was 160 km. The length of the second stage represented a third of the total length of the race. The length of the 4th stage was twice as long as the third stage. What percentage of the to - Determine 8010
 Determine the cone's base's radius if its shell develops into a circular section with radius "s" = 10 and center angle x = 60 °. r = ?, o =?
Determine the cone's base's radius if its shell develops into a circular section with radius "s" = 10 and center angle x = 60 °. r = ?, o =? - Necklaces 8006
 Elena has four beads: yellow, two pink, and green. How many different colored necklaces can he create?
Elena has four beads: yellow, two pink, and green. How many different colored necklaces can he create? - Sheep and cows
 There are only sheep and cows on the farm. Sheep are eight more than cows. The number of cows is half the number of sheep. How many animals live on the farm?
There are only sheep and cows on the farm. Sheep are eight more than cows. The number of cows is half the number of sheep. How many animals live on the farm? - STRESSED word
 Each letter in STRESSED is printed on identical cards, one letter per card, and assembled in random order. Calculate the probability that the cards spell DESSERTS when assembled.
Each letter in STRESSED is printed on identical cards, one letter per card, and assembled in random order. Calculate the probability that the cards spell DESSERTS when assembled. - Direction 7999
 A (5; -4) B (1; 3) C (-2; 0) D (6; 2) Calculate the direction vector a) a = AB b) b = BC c) c = CD
A (5; -4) B (1; 3) C (-2; 0) D (6; 2) Calculate the direction vector a) a = AB b) b = BC c) c = CD - Classroom
 Of the 26 pupils in the classroom, 12 boys and 14 girls, four representatives are picked to the odds of being: a) all the girls b) three girls and one boy c) there will be at least two boys
Of the 26 pupils in the classroom, 12 boys and 14 girls, four representatives are picked to the odds of being: a) all the girls b) three girls and one boy c) there will be at least two boys
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
