Examples for secondary school students - page 37 of 231
Number of problems found: 4608
- What are 3
 What are the five arithmetic means between 2 and 44?
What are the five arithmetic means between 2 and 44? - Jogging program
 After knee surgery, the trainer tells the man to slowly return to his jogging program. He suggests a jogging program for 12 minutes each day for the first week. After that, he suggests increasing the time by 6 minutes per week. Find the number of minutes
After knee surgery, the trainer tells the man to slowly return to his jogging program. He suggests a jogging program for 12 minutes each day for the first week. After that, he suggests increasing the time by 6 minutes per week. Find the number of minutes - Common difference 2
 What is the common difference of the arithmetic sequence with 20 terms, whose first term is 5a+b and the last term is 43a+20 b?
What is the common difference of the arithmetic sequence with 20 terms, whose first term is 5a+b and the last term is 43a+20 b? - Sum of AP members
 Find the sum of all the numbers between 8 and 258 that are divisible by 5.
Find the sum of all the numbers between 8 and 258 that are divisible by 5. - Use AP sum formula
 If x+3x+5x+7x+...+87x=5808, what is the value of x?
If x+3x+5x+7x+...+87x=5808, what is the value of x? - Parabolic sequence
 Find the sum of the first nine terms of an arithmetic sequence whose general term is a(n) = 3n²+5
Find the sum of the first nine terms of an arithmetic sequence whose general term is a(n) = 3n²+5 - The product 9
 The product of the third and second terms of the arithmetic progression is 3000. If the common difference is 10, find the first term.
The product of the third and second terms of the arithmetic progression is 3000. If the common difference is 10, find the first term. - View angle
 We see the tree on the opposite bank of the river at an angle of 15° from a distance of 41 meter from the river bank. From the bank of the river, we can see at an angle of 31°. How tall is the tree?
We see the tree on the opposite bank of the river at an angle of 15° from a distance of 41 meter from the river bank. From the bank of the river, we can see at an angle of 31°. How tall is the tree? - Socks
 Ben's favorite colors are blue and green. He has six blue socks and six green socks in his sock drawer. Unfortunately, they are completely mixed up, and one day, he has to grab some socks to wear in complete darkness. How many socks (minimum) does he have
Ben's favorite colors are blue and green. He has six blue socks and six green socks in his sock drawer. Unfortunately, they are completely mixed up, and one day, he has to grab some socks to wear in complete darkness. How many socks (minimum) does he have - Quadrilateral PQRS
 PQRS is a quadrilateral with P(4,4), S(8,8), and R(12,8). If vector PQ=4*vector SR, find the coordinates of Q. Solve it
PQRS is a quadrilateral with P(4,4), S(8,8), and R(12,8). If vector PQ=4*vector SR, find the coordinates of Q. Solve it - AP five members
 Give the arithmetic sequence of 5 terms if the first term is 8 and the last term is 100. Show your solution.
Give the arithmetic sequence of 5 terms if the first term is 8 and the last term is 100. Show your solution. - Arithmetic mean - parabola
 Find the value of k so that k² + 2k – 3 is the arithmetic mean between k² + 4k + 5 and k² – 6k + 10.
Find the value of k so that k² + 2k – 3 is the arithmetic mean between k² + 4k + 5 and k² – 6k + 10. - Senior students
 There are 7000 students at mountain high school, and 2/7 of these students are seniors. If 2/5 of the seniors favor the school forming a debate team and 3/8 of the remaining students, not seniors, are also forming a debate team, how many students do not f
There are 7000 students at mountain high school, and 2/7 of these students are seniors. If 2/5 of the seniors favor the school forming a debate team and 3/8 of the remaining students, not seniors, are also forming a debate team, how many students do not f - Geometry: 78014
 Good day, Even though it is a trivial task, I don’t know how to deal with it. This is analytic geometry: Find all integers a, b, and c such that the line given by the equation ax+by=c passes through the points [4,3] and [−2,1]. Thank you for your answer
Good day, Even though it is a trivial task, I don’t know how to deal with it. This is analytic geometry: Find all integers a, b, and c such that the line given by the equation ax+by=c passes through the points [4,3] and [−2,1]. Thank you for your answer - The midpoint 3
 The ranges are 10-20, 20-30, 30-40, and 40-50. If the frequency is 7 15 26 12, what is the midpoint?
The ranges are 10-20, 20-30, 30-40, and 40-50. If the frequency is 7 15 26 12, what is the midpoint? - The average 7
 The average lifespan for cricket is 90 days, with a standard deviation of 13 days. If we assume that the lifespan of cricket is normally distributed, a. What is the probability a randomly selected cricket has a lifespan of fewer than 75 days? b. What is t
The average lifespan for cricket is 90 days, with a standard deviation of 13 days. If we assume that the lifespan of cricket is normally distributed, a. What is the probability a randomly selected cricket has a lifespan of fewer than 75 days? b. What is t - Hard equations
 If a<b and c<d and a+b all/2 = c and c+d all/2 = b, and if d-a = 60, what is b-c?
If a<b and c<d and a+b all/2 = c and c+d all/2 = b, and if d-a = 60, what is b-c? - Constructed 77874
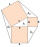 Squares are constructed above the overhangs and the transom. Connecting the outer vertices of adjacent squares creates three triangles. Prove that their areas are the same.
Squares are constructed above the overhangs and the transom. Connecting the outer vertices of adjacent squares creates three triangles. Prove that their areas are the same. - Midpoint of line segment
 Find the midpoint of the line segment joining the points (10,1) and (-8,-1).
Find the midpoint of the line segment joining the points (10,1) and (-8,-1). - The triangle 5
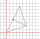 The triangle below has vertices A(-1,-2), B(2,2), and C(-1,4). What is the area of △ABCin square coordinate units?
The triangle below has vertices A(-1,-2), B(2,2), and C(-1,4). What is the area of △ABCin square coordinate units?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
