Examples for secondary school students - page 38 of 231
Number of problems found: 4611
- Constructed 77874
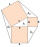 Squares are constructed above the overhangs and the transom. Connecting the outer vertices of adjacent squares creates three triangles. Prove that their areas are the same.
Squares are constructed above the overhangs and the transom. Connecting the outer vertices of adjacent squares creates three triangles. Prove that their areas are the same. - Midpoint of line segment
 Find the midpoint of the line segment joining the points (10,1) and (-8,-1).
Find the midpoint of the line segment joining the points (10,1) and (-8,-1). - The triangle 5
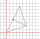 The triangle below has vertices A(-1,-2), B(2,2), and C(-1,4). What is the area of △ABCin square coordinate units?
The triangle below has vertices A(-1,-2), B(2,2), and C(-1,4). What is the area of △ABCin square coordinate units? - Sequence:
 Sequence: 4,10,40,400,16,000,______, ________ Find these two members.
Sequence: 4,10,40,400,16,000,______, ________ Find these two members. - The following 2
 The following data show the number of kilometers joggers ran in a month 4;6;12;12;18;19;25;30;31;40;40;40;40;47;49;60 Find the median of the data.
The following data show the number of kilometers joggers ran in a month 4;6;12;12;18;19;25;30;31;40;40;40;40;47;49;60 Find the median of the data. - A math
 A math teacher teaches Geometry and Precalculus. 37% of students take both math classes, and only 39% take just Geometry. What is the probability that a student will attend Precalculus given that they attended Geometry? What is the percentage of students
A math teacher teaches Geometry and Precalculus. 37% of students take both math classes, and only 39% take just Geometry. What is the probability that a student will attend Precalculus given that they attended Geometry? What is the percentage of students - Underweight babies
 A sample of underweight babies was fed a special diet, and the following weight gains (lbs) were observed at the end of three months: 6.7, 2.7, 2.5, 3.6, 3.4, 4.1, 4.8, 5.9, and 8.3. Find the variance. (Round off to the nearest hundredths)
A sample of underweight babies was fed a special diet, and the following weight gains (lbs) were observed at the end of three months: 6.7, 2.7, 2.5, 3.6, 3.4, 4.1, 4.8, 5.9, and 8.3. Find the variance. (Round off to the nearest hundredths) - Arithmetic seq 2nd grade
 What are the next terms in sequence -1 5 15 29 _ _?
What are the next terms in sequence -1 5 15 29 _ _? - The chief
 The chief fisherman, Peter, estimates that if he uses four lines, then the probability of making a catch on one line is 0.7. If he uses five lines, then the probability of making a catch on any line is 0.6. If he uses six lines, the probability of making
The chief fisherman, Peter, estimates that if he uses four lines, then the probability of making a catch on one line is 0.7. If he uses five lines, then the probability of making a catch on any line is 0.6. If he uses six lines, the probability of making - An insurance
 An insurance company receives, on average, two claims per week from a particular factory. Assuming that a Poisson distribution can model the number of claims, find the probability it receives. three claims in a given week, more than four claims in a given
An insurance company receives, on average, two claims per week from a particular factory. Assuming that a Poisson distribution can model the number of claims, find the probability it receives. three claims in a given week, more than four claims in a given - Yarhands
 Yarhands Statistical Consult conducted statistical analysis on the election results from 1992 to 2012 to assess the chances of the NPP winning the election in Ghana's Volta region. The research reveals that 15% of inhabitants in the Volta region favor the
Yarhands Statistical Consult conducted statistical analysis on the election results from 1992 to 2012 to assess the chances of the NPP winning the election in Ghana's Volta region. The research reveals that 15% of inhabitants in the Volta region favor the - Problem
 Problem Solving: The sum of three consecutive numbers is 93. What is the difference between the largest and the smallest number?
Problem Solving: The sum of three consecutive numbers is 93. What is the difference between the largest and the smallest number? - Bernoulli trial
 A used car saleswoman estimates that each time she shows a customer a car, there is a probability of 0.1 that the customer will buy the car. The saleswoman would like to sell at least one car per week. If showing a car is a Bernoulli trial with a probabil
A used car saleswoman estimates that each time she shows a customer a car, there is a probability of 0.1 that the customer will buy the car. The saleswoman would like to sell at least one car per week. If showing a car is a Bernoulli trial with a probabil - Dipole - complex power
 For a dipole, calculate the complex apparent power S and the instantaneous value of the current i(t), given: R=10 Ω, C=100uF, f=50 Hz, u(t)= square root of 2 * sin( ωt - 30°). Thanks for any help or advice.
For a dipole, calculate the complex apparent power S and the instantaneous value of the current i(t), given: R=10 Ω, C=100uF, f=50 Hz, u(t)= square root of 2 * sin( ωt - 30°). Thanks for any help or advice. - Find all
 Find all right-angled triangles whose side lengths form an arithmetic sequence.
Find all right-angled triangles whose side lengths form an arithmetic sequence. - There 25
 There are four red marbles and six blue marbles in a bag. What is the probability of picking up one blue marble and then one red marble? (assume that you keep the blue marble out of the bag)
There are four red marbles and six blue marbles in a bag. What is the probability of picking up one blue marble and then one red marble? (assume that you keep the blue marble out of the bag) - Five friends
 Five friends ate a 12-slice pizza. Samir ate three times as many slices as Joe. Joe ate half as many slices as Emily. Kendra and Fong together ate half a pizza. Kendra ate one-third as many slices as Samir. Fong ate the most slices. What fraction of a piz
Five friends ate a 12-slice pizza. Samir ate three times as many slices as Joe. Joe ate half as many slices as Emily. Kendra and Fong together ate half a pizza. Kendra ate one-third as many slices as Samir. Fong ate the most slices. What fraction of a piz - Conditional probability
 Suppose a batch contains ten items, of which four are defective. Two items are drawn at random from the batch, one after the other, without replacement. What is the probability that: I) Both are defective? Ii) Is the second item defective?
Suppose a batch contains ten items, of which four are defective. Two items are drawn at random from the batch, one after the other, without replacement. What is the probability that: I) Both are defective? Ii) Is the second item defective? - A fair coin
 A fair coin is tossed twice. Write down the set of possible outcomes. What is the probability of obtaining it? I. Exactly one head ii. No head
A fair coin is tossed twice. Write down the set of possible outcomes. What is the probability of obtaining it? I. Exactly one head ii. No head - A triangle 6
 A triangle has vertices on a coordinate grid at H(-2,7), I(4,7), and J(4,-9). What is the length, in units, of vector HI?
A triangle has vertices on a coordinate grid at H(-2,7), I(4,7), and J(4,-9). What is the length, in units, of vector HI?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
