Examples for secondary school students - page 70 of 231
Number of problems found: 4610
- Potential 42561
 The elevator cabin weighing 720 kg goes from the ground floor to the top floor of the building, at 125 m. How much potential energy does the elevator cabin have on the top floor of the building - at the height of 125 m?
The elevator cabin weighing 720 kg goes from the ground floor to the top floor of the building, at 125 m. How much potential energy does the elevator cabin have on the top floor of the building - at the height of 125 m? - Harry
 Harry Thomson bought a large land in the shape of a rectangle with a circumference of 90 meters. He divided it into three rectangular plots. The shorter side has all three plots of equal length. Their longer sides are three consecutive natural numbers. Fi
Harry Thomson bought a large land in the shape of a rectangle with a circumference of 90 meters. He divided it into three rectangular plots. The shorter side has all three plots of equal length. Their longer sides are three consecutive natural numbers. Fi - Alcohol risk
 The 2009 Youth Risk Behavior Survey found that about 5 out of 12 high school students drank some alcohol in the 30 days preceding the survey. If a high school has 2400 students, how many would be expected to have used alcohol within 30 days?
The 2009 Youth Risk Behavior Survey found that about 5 out of 12 high school students drank some alcohol in the 30 days preceding the survey. If a high school has 2400 students, how many would be expected to have used alcohol within 30 days? - Functions 42201
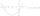 Y = x² + 4x-2 Quadratic functions Calculate and graph.
Y = x² + 4x-2 Quadratic functions Calculate and graph. - Radiators
 Calculate the radiator output if it has a thermal gradient (difference between inlet water and return temperatures) a) 5°C b) 10°C c) 15°C d) 20°C A heating water volume flow is 45 kg/h. How fast the water flows from the supply pipe to the radiator e) DN1
Calculate the radiator output if it has a thermal gradient (difference between inlet water and return temperatures) a) 5°C b) 10°C c) 15°C d) 20°C A heating water volume flow is 45 kg/h. How fast the water flows from the supply pipe to the radiator e) DN1 - Modulus and argument
 Find the mod z and argument z if z=i
Find the mod z and argument z if z=i - Three-digit numbers
 How many three-digit numbers are not closer to 600 on the number axis than 400?
How many three-digit numbers are not closer to 600 on the number axis than 400? - Free fall
 The elevator car weighing 720 kg, is torn off at the height of 125 m and begins to fall in a free fall. How much kinetic energy did the elevator car have when it hit the ground floor of the building when the free fall of the car lasted 5 s?
The elevator car weighing 720 kg, is torn off at the height of 125 m and begins to fall in a free fall. How much kinetic energy did the elevator car have when it hit the ground floor of the building when the free fall of the car lasted 5 s? - Perpendicular leg
 Calculate the area of a right triangle whose longer perpendicular is six dm shorter than the hypotenuse and three dm longer than the shorter perpendicular.
Calculate the area of a right triangle whose longer perpendicular is six dm shorter than the hypotenuse and three dm longer than the shorter perpendicular. - Giraffe 2
 The lifespan of a guinea pig is six years less than that of a giraffe. The lifespan of a tiger is four times that of a guinea pig. If the total lifespan of the animals is 30 years, calculate the longevity of the giraffe.
The lifespan of a guinea pig is six years less than that of a giraffe. The lifespan of a tiger is four times that of a guinea pig. If the total lifespan of the animals is 30 years, calculate the longevity of the giraffe. - Free fall 5
 Jeremy accidentally dropped his toy stuffed animal from the balcony of his apartment on the fourth floor. The toy hit the ground at a velocity of 16.0 meters per second. At impact, it took 2.0 seconds for the toy's velocity to reach 0 meters per second. I
Jeremy accidentally dropped his toy stuffed animal from the balcony of his apartment on the fourth floor. The toy hit the ground at a velocity of 16.0 meters per second. At impact, it took 2.0 seconds for the toy's velocity to reach 0 meters per second. I - Permutations with repetitions
 How many times can the input of 1.2.2.3.3.3.4 be permutated into four digits, three digits, and two digits without repetition? Ex: 4 digits = 1223, 2213, 3122, 2313, 4321. . etc 3 digits = 122.212.213.432. . etc 2 digits = 12, 21, 31, 23 I have tried the
How many times can the input of 1.2.2.3.3.3.4 be permutated into four digits, three digits, and two digits without repetition? Ex: 4 digits = 1223, 2213, 3122, 2313, 4321. . etc 3 digits = 122.212.213.432. . etc 2 digits = 12, 21, 31, 23 I have tried the - Saving in January
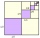 On the 1st of January, a student puts $10 in a box. On the 2nd, she puts $20 in the box, and so on, putting the same number of 10-dollars notes as the day of the month. How much money will be in the box if she keeps doing this for a) the first ten days of
On the 1st of January, a student puts $10 in a box. On the 2nd, she puts $20 in the box, and so on, putting the same number of 10-dollars notes as the day of the month. How much money will be in the box if she keeps doing this for a) the first ten days of - Arithmetic progression 2
 The 3rd term of an Arithmetic progression is ten more than the first term, while the fifth term is 15 more than the second term. Find the sum of the 8th and 15th terms of the Arithmetic progression if the 7th term is seven times the first term.
The 3rd term of an Arithmetic progression is ten more than the first term, while the fifth term is 15 more than the second term. Find the sum of the 8th and 15th terms of the Arithmetic progression if the 7th term is seven times the first term. - The town
 The town population is 56000. It is decreasing by 2% every year. What will be the population of the town after 13 years?
The town population is 56000. It is decreasing by 2% every year. What will be the population of the town after 13 years? - Tests
 To obtain a grade A, Patrick must score an average of at least 70 on five tests. If his average mark for the four tests is 68, what is the lowest mark he can get on his fifth test and still obtain a grade A
To obtain a grade A, Patrick must score an average of at least 70 on five tests. If his average mark for the four tests is 68, what is the lowest mark he can get on his fifth test and still obtain a grade A - Maturity value
 IKEA Furniture can purchase furniture with a three-year simple interest loan at 8% interest per year. What is the maturity value of a 3500 loan?
IKEA Furniture can purchase furniture with a three-year simple interest loan at 8% interest per year. What is the maturity value of a 3500 loan? - The sides
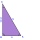 The sides of a right triangle form an arithmetic sequence. The hypotenuse is 24 cm long. Determine the remaining sides of the triangle.
The sides of a right triangle form an arithmetic sequence. The hypotenuse is 24 cm long. Determine the remaining sides of the triangle. - Binary words
 How many 10-bit words can be created with precisely four units (e.g., 1111000000)?
How many 10-bit words can be created with precisely four units (e.g., 1111000000)? - Exchange € 100
 Find out how many ways you can exchange € 100 if you have an unlimited number of 50, 20, 10, and 5 euro banknotes. Use a method other than listing all options systematically.
Find out how many ways you can exchange € 100 if you have an unlimited number of 50, 20, 10, and 5 euro banknotes. Use a method other than listing all options systematically.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
