Sleep vs. watch TV time
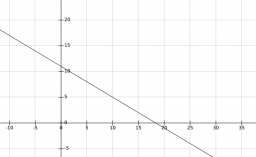
Using a data set relating to the number of episodes I watch on TV in a day (x) versus the number of hours of sleep I get that night (y), I construct the linear model
y=−0.6x+11
Which of the following general observations can you make from this model?
a) If I watch more TV, I generally sleep less.
b) If I watch more TV, I generally sleep more.
c) If I watch less TV, I generally sleep less.
y=−0.6x+11
Which of the following general observations can you make from this model?
a) If I watch more TV, I generally sleep less.
b) If I watch more TV, I generally sleep more.
c) If I watch less TV, I generally sleep less.
Final Answer:
Tips for related online calculators
Do you want to convert time units like minutes to seconds?
You need to know the following knowledge to solve this word math problem:
geometrybasic operations and conceptsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Natural numbers
Find the number of all natural numbers greater than 200 in which the digits 1, 2, 4, 6, 8 occur at most once and not contains any other digits. - Distance of the parallels
Find the distance of the parallels, which equations are: x = 3-4t, y = 2 + t and x = -4t, y = 1 + t (instructions: select a point on one line and find its distance from the other line) - Bivariate data set
Here is a bivariate data set in which you believe y to be the response variable. x y 51.4 44.8 60.2 46.6 60.1 46.8 45.8 46.3 37.4 41.8 72.4 52.5 60 48.2 67.5 49.5 60.9 49.8 51.1 45.7 62.7 49.6 194.9 84.2 Make a scatter plot of this data. Which point is an - An insurance
An insurance company receives, on average, two claims per week from a particular factory. Assuming that a Poisson distribution can model the number of claims, find the probability it receives. three claims in a given week, more than four claims in a given - Milk mixture
In a container, milk and water are 7:5. If 15 L water is added, the ratio becomes 7:8. Find the quantity of water in the new mixture. - Linear imaginary equation
Given that 2(z+i)=i(z+i) "this is z star" Find the value of the complex number z. - Linear function
Write the following problems using x as the unknown variable, using one of the following forms: x+p=q or px=q. Larry ran seven more miles than Barry in a month; if Larry ran 20 miles, how many did Barry run?
