Derivation - practice problems
Direction: Solve each problem carefully and show your solution in each item.Number of problems found: 48
- Tent - spherical cap
I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What - Dogde Caliber
The petrol kilometers M (unit: kilometers per liter) of the Dodge Caliber car is modeled by the function: M(s) = - 1/28s² + 3s- 31 What is the car's best petrol kilometers, and what speed is attained? - Acceleration 83304
The acceleration of a mass point during its rectilinear movement decreases uniformly from the initial value a0 = 10 m/s2 at time t0 = 0 to a zero value for a period of 20 s. What is the speed of the mass point at time t1 = 20 s, and what is the path of th - Accelerated motion
The position of a mass point that moves along the x-axis is given by the relation x=10t²-5t. Express its velocity and acceleration. - L Hospital's rule
Use L Hospital's rule to solve (i) Lim x²+5x-14/x²-5x+6 X—>2 (ii)Lim x³+x²-x-1/x²-2x-3 X—>3 - A particle 2
If the motion of a particle is described by the relation a(t) = 7t³ + 2 m/s², and the initial velocity of the motion is zero when t = 0 and the distance is 2m, t = 0.5s. Determine the velocity and displacement when t = 10s. - Parabola with abs
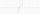A). Sketch the graph of the function f(x)=x * absolute(x) = x * |x| b). For what values of x is f(x) differentiable c). Find F(x)
- Intersection of Q2 with line
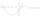The equation of a curve C is y=2x² - 8x +9, and the equation of a line L is x + y=3. (1) Find the x-coordinates of the points of intersection of L and C. (ii) show that one of these points is also the - Function x*tanx
Functions: f(x)=xtanx f(x)=(e^x)/((e^x)+1) Find; i)vertical and horizontal asymptotes iii)the interval of decrease and increase iii)Local maxima and local minima iv)interval of concavity and inflection. And sketch the graph. - The MRT train
The MRT running from Taft to North Avenue has a starting velocity of 60km/hr. After a malfunction, the brakes failed, making the train run at a velocity of 80km/hr. What is the acceleration rate if the time for velocity change is 5 seconds? - Penny free fall
A man drops a penny from the top of a 500m tall building. After t seconds, the penny has fallen a distance of s meters, where s(t)=500-5t². Determine the average velocity between 1s and 5s. - Martians
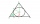A sphere-shaped spaceship with a diameter of 6 m landed in the meadow. To avoid attracting attention, the Martians covered it with a roof in the shape of a regular cone. How high will this roof be so that the consumption of roofing is minimal? - Megapizza
Mega pizza will be divided among 100 people. First gets 1%, 2nd 2% of the remainder, 3rd 3% of the remainder, etc. Last 100th 100% of the remainder. Which person got the biggest portion? - Sleep vs. watch TV time
Using a data set relating to the number of episodes I watch on TV in a day (x) versus the number of hours of sleep I get that night (y), I construct the linear model y=−0.6x+11 Which of the following general observations can you make from this model? a) I - Ascend vs. descent
Which function is growing? a) y = 2-x b) y = 20 c) y = (x + 2). (-5) d) y = x-2
- Maximum of volume
The shell of the cone is formed by winding a circular section with a radius of 1. For what central angle of a given circular section will the volume of the resulting cone be maximum? - The shooter
The shooter shoots at the target, assuming that the individual shots are independent of each other and the probability of hitting them is 0.2. The shooter fires until he hits the target for the first time, then stops firing. (a) What is the most likely nu - Derivative problem
The sum of two numbers is 12. Find these numbers if: a) The sum of their third powers is minimal. b) The product of one with the cube of the other is maximal. c) Both are positive, and the product of one with the other power of the other is maximal. - Shopping malls
The chain of department stores plans to invest up to 24,000 euros in television advertising. Ads will place all commercials on a television station where the broadcast of a 30-second spot costs EUR 1,000 and is watched by 14,000 potential customers. Durin - Secret treasure
Scouts have a tent in the shape of a regular quadrilateral pyramid with a side of the base of 4 m and a height of 3 m. Find the container's radius r (and height h) so that they can hide the largest possible treasure.
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
