Maximum of volume
The shell of the cone is formed by winding a circular section with a radius of 1. For what central angle of a given circular section will the volume of the resulting cone be maximum?
Your answer:
Your answer:
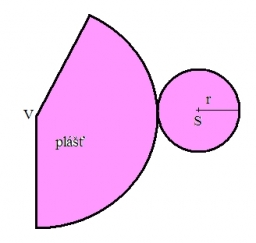
Tips for related online calculators
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetrybasic operations and conceptsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Circle arc + section
Calculate the length of the arc of a circle and the volume of a circular section if the circle's radius is 8.3 centimeters and the central angle alpha=104 degrees. - Cone Radius Sector Angle
Determine the cone's base's radius if its shell develops into a circular section with radius "s" = 10 and center angle x = 60 °. r = ?, o =? - Cut and cone
Calculate the volume of the rotation cone whose lateral surface is a circular arc with radius 15 cm and central angle 63 degrees. - Circular grass seed
How many kg of grass seed must be bought to start a lawn in the shape of a circular section with a radius of r= 15 m and a central angle of 45 degrees if 1 g of grass seed is used per 1 dm of the square area? - Circular segment
What is the radius of a circular section whose central angle is 36° and the area of S = 53.095 cm²? - Cross-sections of a cone
Cone with base radius 15 cm and height 20 cm divided by parallel planes to base into three bodies. The planes divide the height of the cone into three equal parts. Determine the volume ratio of the maximum and minimum of the resulting body. - Angle of cone
The cone has a base diameter of 1.5 m. The angle at the central apex of the axial section is 86°. Calculate the volume of the cone.
