Secret treasure

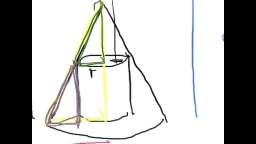
Scouts have a tent in the shape of a regular quadrilateral pyramid with a side of the base 4 m and a height of 3 m. Find the container's radius r (and height h) so that they can hide the largest possible treasure.

Correct answer:

r =  1.3333 m
h =  1 m

Step-by-step explanation:

$$\begin{gathered} a=4\text{ m } \\ v=3\text{ m } \\ {s}^2=(a\mathrm{/}2{)}^2+v^2 \\ s=\sqrt{(a\mathrm{/}2{)}^2+v^2}=\sqrt{(4\mathrm{/}2{)}^2+3^2}=\sqrt{13}\text{ m}\doteq 3.6056\text{ m } \\ (v-h):r=v:a\mathrm{/}2 \\ v=h+r\cdot v:a\mathrm{/}2 \\ h=v-r\cdot 2v\mathrm{/}a \\ V=\pi r^{2}h \\ V=\pi r^2(v-r\cdot 2v\mathrm{/}a) \\ V=\pi r^2(v-r\cdot 2v\mathrm{/}a) \\ V=\pi r^2(3-r\cdot 2\cdot 3\mathrm{/}4) \\ {V}^{\mathrm{\prime }}=3\mathrm{/}2\pi (a-vr)r \\ {V}^{\mathrm{\prime }}=0 \\ 3\mathrm{/}2\pi \cdot (a-vr)r=0 \\ 3\mathrm{/}2\ast pi\ast (4-3r)r=0 \\ 3\mathrm{/}2\cdot 3.1415926\cdot (4-3r)r=0 \\ -14.1371667r^2+18.85r=0 \\ 14.1371667r^2-18.85r=0 \\ a=14.1371667;b=-18.85;c=-0 \\ D=b^2-4ac=18.85^2-4\cdot 14.1371667\cdot -0=355.305746317 \\ D>0 \\ {r}_{1,2}={\displaystyle \frac{-b\pm \sqrt{D}}{2a}}={\displaystyle \frac{18.85\pm \sqrt{355.31}}{28.2743334}} \\ {r}_{1,2}=0.66666667\pm 0.666666666667 \\ {r}_1=1.33333333333 \\ {r}_2=0 \\ \text{ Factored form of the equation: } \\ 14.1371667(r-1.33333333333)r=0 \\ r=r_1=1.3333={\displaystyle \frac{4}{3}}=1.3333\text{ m} \end{gathered}$$

Our quadratic equation calculator calculates it.

$h=v-r\cdot 2\cdot v\mathrm{/}a=3-1.3333\cdot 2\cdot 3\mathrm{/}4=1\text{ m}$

Try another example

Related math problems and questions:

• The tent
  Calculate how much cover (without a floor) is used to make a tent that has the shape of a regular square pyramid. The edge of the base is 3 m long and the height of the tent is 2 m.
• Quadrilateral pyramid
  A regular quadrilateral pyramid has a volume of 24 dm³ and a base edge a = 4 dm. Calculate: a/height of the pyramid b/sidewall height c/surface of the pyramid
• Cylindrical container
  An open-topped cylindrical container has a volume of V = 3140 cm³. Find the cylinder dimensions (radius of base r, height v) so that the least material is needed to form the container.
• Triangular pyramid
  What is the volume of a regular triangular pyramid with a side 3 cm long?
• The tent
  The tent shape of a regular quadrilateral pyramid has a base edge length a = 2 m and a height v = 1.8 m. How many m² of cloth we need to make the tent if we have to add 7% of the seams? How many m³ of air will be in the tent?
• The quadrilateral pyramid
  The quadrilateral pyramid has a rectangular base of 24 cm x 3.2dm and a body height of 0.4m. Calculate its volume and surface area.
• Tent
  Calculate how many liters of air will fit in the tent that has a shield in the shape of an isosceles right triangle with legs r = 3 m long the height = 1.5 m and a side length d = 5 m.
• Alien ship
  The alien ship has the shape of a sphere with a radius of r = 3000m, and its crew needs the ship to carry the collected research material in a cuboid box with a square base. Determine the length of the base and (and height h) so that the box has the large
• Regular 4-sided pyramid
  Find the area (surface area) of a regular 4-sided pyramid if its height is 20 m and the wall height is 23 m.
• Pyramid cut
  We cut the regular square pyramid with a parallel plane to the two parts (see figure). The volume of the smaller pyramid is 20% of the volume of the original one. The bottom of the base of the smaller pyramid has a content of 10 cm². Find the area of the
• Distance of points
  A regular quadrilateral pyramid ABCDV is given, in which edge AB = a = 4 cm and height v = 8 cm. Let S be the center of the CV. Find the distance of points A and S.
• Triangular pyramid
  A regular tetrahedron is a triangular pyramid whose base and walls are identical equilateral triangles. Calculate the height of this body if the edge length is a = 8 cm
• Find the
  Find the surface area of a regular quadrilateral pyramid which has a volume of 24 dm³ and a height of 45 cm.
• Quadrilateral pyramid
  We have a regular quadrilateral pyramid with a base edge a = 10 cm and a height v = 7 cm. Calculate 1/base content 2/casing content 3/pyramid surface 4/volume of the pyramid
• Quadrilateral pyramid
  In a regular quadrilateral pyramid, the height is 6.5 cm and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body. Round calculations to 1 decimal place.
• The pyramid
  The pyramid with a square base is 50 m high and the height of the sidewall is 80 m. Find the endge of the base of the pyramid.
• 4side pyramid
  Calculate the volume and surface of 4 sides regular pyramid whose base edge is 4 cm long. The angle from the plane of the sidewall and base plane is 60 degrees.