Alien ship
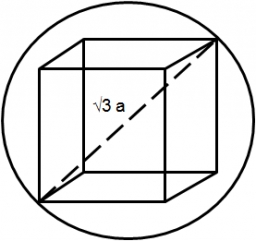
The alien ship has the shape of a sphere with a radius of r = 3000m, and its crew needs the ship to carry the collected research material in a cuboid box with a square base. Determine the length of the base and (and height h) so that the box has the largest possible volume.
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
- arithmetic
- cube root
- third power
- solid geometry
- cuboid
- sphere
- prism
- planimetrics
- square
- basic functions
- derivation
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Confectionery 7318
The confectioner needs to carve a cone-shaped decoration from a ball-shaped confectionery mass with a radius of 25 cm. Find the radius of the base of the ornament a (and the height h). He uses as much material as possible is used to make the ornament. - Secret treasure
Scouts have a tent in the shape of a regular quadrilateral pyramid with a side of the base of 4 m and a height of 3 m. Find the container's radius r (and height h) so that they can hide the largest possible treasure. - Cylindrical container
An open-topped cylindrical container has a volume of V = 3140 cm³. Find the cylinder dimensions (radius of base r, height v) so that the least material is needed to form the container. - Surface and volume od cuboid
The square base of the cuboid has an area of Sp = 36 cm2, and its height is 80 mm. Determine its surface area and volume.
- Church roof
The roof of the church tower has the shape of a regular tetrahedral pyramid with a base edge length of 5.4 meters and a height of 5 m. It was found that the 27% covering of the roof area needs to be corrected. What amount of material will be required? - Four prisms
Question No. 1: The prism has the dimensions a = 2.5 cm, b = 100 mm, c = 12 cm. What is its volume? a) 3000 cm² b) 300 cm² c) 3000 cm³ d) 300 cm³ Question No.2: The prism base is a rhombus with a side length of 30 cm and a height of 27 cm. The height of t - Percentage 3481
We turned a sphere with the largest possible radius from a cube with an edge length of 8 cm. Calculate the volume of the cube, the ball, and the percentage of waste when turning.
