Poklad

Skauti majú stan v tvare pravidelného štvorbokého ihlanu so stranou podstavy 4 m a výške 3 m. Do stanu potrebujú schovať valcovú nádobu s tajným pokladom. Určte polomer r (a výšku h) nádoby tak, aby mohli schovať čo nejobjemnější poklad.

Správna odpoveď:

r =  1,3333 m
h =  1 m

Postup správneho riešenia:

Výpočet overte naším kalkulátorom kvadratických rovníc .

$h=v-r\cdot 2\cdot v\mathrm{/}a=3-1.3333\cdot 2\cdot 3\mathrm{/}4=1\text{ m}$

Skúsiť iný príklad

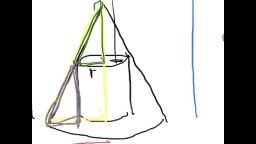
Zobrazujem 2 komentáre:

Žiak

Nie je dobre vyriešený príklad.

1 rok  Like

Matematik

Ahoj, a co konkretne je nespravne? Skontroloval som aj podobnost trojuholnikov - ok. Aj derivovanie aj najdenie maxima. Aj wolfram najde maximum objemu  rovnake:

https://www.wolframalpha.com/input/?i=maximum+%CF%80*r%5E2+*%283%E2%88%92r*2*3%2F4%29+

1 rok  Like

Súvisiace a podobné príklady:

• Plocha stanu
  Vypočítaj, koľko plátna ( bez podlahy ) sa spotrebuje na zhotovenie stanu, ktorý má tvar pravidelného štvorbokého ihlana. Hrana podstavy má dĺžku 3 m a výška stanu je 2m .
• V rekreačnej
  V rekreačnej oblasti sa má postaviť bazén v tvare kvádra s objemom 200m³. Jeho dĺžka má byť 4- násobkom šírky, pričom cena 1 m² dna bazéna je 2- krát lacnejšia ako 1 m² steny bazéna. Aké rozmery musí mať bazén, aby stavba bola najlacnejšia?
• 3boký ihlan
  Aký je objem pravidelného trojbokého ihlanu so stranou 3cm?
• Stan
  Stan tvaru pravidelného štvorbokého ihlanu má dĺžku podstavnej hrany a = 2m a výšku v = 1,8m. Koľko m² plátna potrebujeme na ušitie stanu, ak musíme chcete pridať 7% na švy? Koľko m³ vzduchu bude v stane?
• Parabolický úsek
  Parabolický úsek má základňu a = 4 cm a výšku v = 6 cm. Vypočítajte objem telesa, ktoré vznikne rotáciou tejto úseče a) okolo svojej základne b) okolo svojej osi. Vopred ďakujem za riešenie.
• Ihlan 4b
  Vypočítajte povrch S a objem V pravidelného štvorbokého ihlanu so stranou podstavy a = 5 m a telesovou výškou 14 m.
• Rez ihlana
  Pravidelný ihlan so štvorcovou podstavou rozrežeme rovinou rovnobežnou s podstavou na dve časti (pozrite obrázok). Objem vzniknutého menšieho ihlana tvorí 20 % objemu pôvodného ihlana. Podstava vzniknutého menšieho ihlana má obsah 10 cm². Určte v centimet
• Ukážte 2
  Ukážte (pomocou Menealovej vety), že ťažisko delí ťažnicu v pomere 1:2.
• Valcové príklady
  1. Určte rozmery valcovej nádoby s objemom 5 litrov, ak výška nádoby sa rovná polomeru podstavy. 2. V pohári valcovitého tvaru s vnútorným priemerom 8 cm sú 3 dl džúsu. Vypočítajte plochu džúsom zmáčanej časti pohára. 3. Konzerva s uhorkami má tvar valca.
• Guľa
  Získajte rovnicu guľovej plochy so stredom na čiare 3x + 2z = 0 = 4x-5y a prechádza bodmi (0, -2, -4) a (2, -1,1).
• Lichobežník plocha
  Plocha lichobežníka je 266. Čo je hodnota x ak sú základne dlhé: b1 je 2x-3, b2 je 2x + 1 a výška h je x + 4
• Výška valca
  Vypočitajte výšku valca ak jeho povrch je 2500 dm² a podstavy majú priemer 5dm.
• Stan 6
  Koľko m² látky treba na zhotovenie stanu pravidelného 3-bokeho hranola ak treba počítať s 2%rezervou látky? Rozmery - 2m 1,6m a výška 1,4 m
• Je štvorboký
  Je štvorboký ihlan, ktorý má podstavu obdĺžnik s rozmermi 24cm, 13cm. Výška ihlanu je 18cm. Vypočítajte: 1/obsah podstavy 2/obsah plášťa 3/povrch ihlanu 4/objem ihlanu
• Štvorboký
  Pravidelný štvorboký ihlan má objem 24dm³ a podstavnou hranu a = 4 dm. Vypočítajte: a/výšku ihlanu b/výšku pobočnom steny c/povrch ihlanu
• Stan iglu
  Stan v tvare kužeľa je vysoký 3 m, priemer jeho podstavy je 3,2 m. a) Stan je vyrobený je z dvoch vrstiev materiálu. Koľko m² látky treba na výrobu (vrátane podlahy), ak k minimálnemu množstvu treba kvôli odpadu pri strihaní pridať 20 %? b) Koľko m³ vzduc
• Stan 8
  Stan tvaru ihlana má podstavu štvoreca s veľkosťou strany 2,2m a výšku 1,8m. Koľko metrov štvorcových stanového plátna je treba na jeho zhotovenie ak počítame päť percent naviac na založenie?