Length + surface area - practice problems
Number of problems found: 227
- A frustum
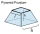 A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume.
A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume. - A cone 3
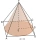 A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain.
A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain. - Calculation 83339
 The edges of a cuboid are in the ratio 1:2:3. Calculate their length if you know that the surface of the entire cuboid is S=5632 m². Then, perform a test to ensure the calculation is correct.
The edges of a cuboid are in the ratio 1:2:3. Calculate their length if you know that the surface of the entire cuboid is S=5632 m². Then, perform a test to ensure the calculation is correct. - Quadrilateral 83324
 The volume of a regular quadrilateral pyramid is 72 cm³. Its height is equal to the length of the base edge. Calculate the length of the base and the surface of the pyramid.
The volume of a regular quadrilateral pyramid is 72 cm³. Its height is equal to the length of the base edge. Calculate the length of the base and the surface of the pyramid.
- Calculate 82700
 A cone of rotation with a radius of 32 cm and side length s = 65 cm is given. Calculate the surface area and volume.
A cone of rotation with a radius of 32 cm and side length s = 65 cm is given. Calculate the surface area and volume. - Calculate 82690
 A cone of rotation with a height of 18 cm and side length s = 45 cm is given. Calculate the surface area and volume.
A cone of rotation with a height of 18 cm and side length s = 45 cm is given. Calculate the surface area and volume. - Semicircle 82687
 If the shell of a cone is a semicircle, then the diameter of the cone's base is equal to its side's length. Prove it.
If the shell of a cone is a semicircle, then the diameter of the cone's base is equal to its side's length. Prove it. - Equilateral 82576
 Calculate the volume and surface area of a 9.6 cm high prism with a base of an equilateral triangle of length 4.8 cm.
Calculate the volume and surface area of a 9.6 cm high prism with a base of an equilateral triangle of length 4.8 cm. - Calculate 82549
 The cylinder has a shell surface of 88 square cm and a volume of 176 cubic cm. Calculate the radius, height, and surface area of the given solid.
The cylinder has a shell surface of 88 square cm and a volume of 176 cubic cm. Calculate the radius, height, and surface area of the given solid.
- Determine 82032
 Determine the volume and surface area of a cone whose slope of length 8 cm makes an angle of 75 degrees with the plane of the base.
Determine the volume and surface area of a cone whose slope of length 8 cm makes an angle of 75 degrees with the plane of the base. - Cantilevers 81937
 Calculate a prism's volume and surface area with a base of a right triangle with cantilevers of length 40 and 43 cm. The height of the prism is 60 cm.
Calculate a prism's volume and surface area with a base of a right triangle with cantilevers of length 40 and 43 cm. The height of the prism is 60 cm. - Cross-section 81879
 The castle has a length of 4 m and a cross-section in the shape of a square whose side is 15 cm long. Eight such castles must be painted. One kilogram can is enough for 6 m² of coating. How many cans of paint should be bought?
The castle has a length of 4 m and a cross-section in the shape of a square whose side is 15 cm long. Eight such castles must be painted. One kilogram can is enough for 6 m² of coating. How many cans of paint should be bought? - Identical 81642
 What is the largest surface area of a square glued together from 12 identical cubes with an edge length of 1 cm?
What is the largest surface area of a square glued together from 12 identical cubes with an edge length of 1 cm? - Centimeters 81623
 The warehouse has the shape of a cuboid with dimensions: length of 50 meters, width of 600 decimeters, and height of 300 centimeters. Calculate how much it will cost to paint a windowless room with a door 150 centimeters wide and 200 centimeters high (the
The warehouse has the shape of a cuboid with dimensions: length of 50 meters, width of 600 decimeters, and height of 300 centimeters. Calculate how much it will cost to paint a windowless room with a door 150 centimeters wide and 200 centimeters high (the
- Calculate 80995
 Calculate the cube's surface with the edges of the length: 2 half cm, 3.5 cm; it is a quarter of a cm.
Calculate the cube's surface with the edges of the length: 2 half cm, 3.5 cm; it is a quarter of a cm. - Expressed 79474
 The length of the cube's edge in cm is expressed as a natural number. Its volume is greater than 100 and less than 200. Calculate the surface area of the cube.
The length of the cube's edge in cm is expressed as a natural number. Its volume is greater than 100 and less than 200. Calculate the surface area of the cube. - Surface 72394
 The volume of the cube is 15625 cubic meters. Find the length of the edge and the surface of the cube.
The volume of the cube is 15625 cubic meters. Find the length of the edge and the surface of the cube. - Cube-shaped 71414
 Mother and daughter Susan are wrapping presents for father. Maťko has a cube-shaped box with dimensions of 9 cm, 3 cm, and 7 cm, and Zuzka has a box in the shape of a cube with an edge length of 3 cm. How many square cm of wrapping paper will they use in
Mother and daughter Susan are wrapping presents for father. Maťko has a cube-shaped box with dimensions of 9 cm, 3 cm, and 7 cm, and Zuzka has a box in the shape of a cube with an edge length of 3 cm. How many square cm of wrapping paper will they use in - Considering 67324
 Susan has an old stool - a cube with an edge length of 80 cm. She wants to sew a new cover for her. How many square meters does the fabric consume, considering adding 15% for stitching and folds?
Susan has an old stool - a cube with an edge length of 80 cm. She wants to sew a new cover for her. How many square meters does the fabric consume, considering adding 15% for stitching and folds?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
Do you want to convert length units? Length - practice problems. Examples for the calculation of the surface area of the solid object .
