Practice problems of the surface area of a pyramid
Number of problems found: 140
- Januka
 Januka and her father were going to the tent. They found that their old tent was torn. Their mother suggested that they sew a tent whose walls would be made of 4 identical isosceles triangles. Their lower side is 2 m long, and the height is also 2 m. Then
Januka and her father were going to the tent. They found that their old tent was torn. Their mother suggested that they sew a tent whose walls would be made of 4 identical isosceles triangles. Their lower side is 2 m long, and the height is also 2 m. Then - A cone 3
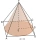 A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain.
A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain. - A frustum
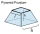 A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume.
A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume. - Storage shed
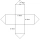 Frank designed a net for a storage shed that he is going to construct out of metal. The design consists of a square base and four square sides, plus four triangular parts that make up the roof. A square base of 6 feet and four square sides, plus 4 feet of
Frank designed a net for a storage shed that he is going to construct out of metal. The design consists of a square base and four square sides, plus four triangular parts that make up the roof. A square base of 6 feet and four square sides, plus 4 feet of
- Pentagonal pyramid
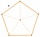 Find the volume and surface of a regular pentagonal pyramid with a base edge a = 12.8 cm and a height v = 32.1 cm.
Find the volume and surface of a regular pentagonal pyramid with a base edge a = 12.8 cm and a height v = 32.1 cm. - Top of the tower
 The top of the tower has the shape of a regular hexagonal pyramid. The base edge has a length of 1.2 m. The pyramid height is 1.6 m. How many square meters of sheet metal are needed to cover the top of the tower if 15% extra sheet metal is needed for join
The top of the tower has the shape of a regular hexagonal pyramid. The base edge has a length of 1.2 m. The pyramid height is 1.6 m. How many square meters of sheet metal are needed to cover the top of the tower if 15% extra sheet metal is needed for join - Isosceles 3551
 Jan and her father were going to the tent. They found that their old tent is torn. Their mother suggested that they sew a tent whose walls would be made up of six identical isosceles triangles. Their lower side is 2 m long, and the height to this side mea
Jan and her father were going to the tent. They found that their old tent is torn. Their mother suggested that they sew a tent whose walls would be made up of six identical isosceles triangles. Their lower side is 2 m long, and the height to this side mea - The roof
 The tower's roof has the shape of a regular quadrangular pyramid, the base edge of which is 11 m long, and the side wall of the animal with the base at an angle of 57°. Calculate how much roofing we need to cover the entire roof if we count on 15% waste.
The tower's roof has the shape of a regular quadrangular pyramid, the base edge of which is 11 m long, and the side wall of the animal with the base at an angle of 57°. Calculate how much roofing we need to cover the entire roof if we count on 15% waste. - The tent
 The tent shape of a regular quadrilateral pyramid has a base edge length a = 2 m and a height v = 1.8 m. How many m² of cloth did we need to make the tent if we have to add 7% of the seams? How many m³ of air will be in the tent?
The tent shape of a regular quadrilateral pyramid has a base edge length a = 2 m and a height v = 1.8 m. How many m² of cloth did we need to make the tent if we have to add 7% of the seams? How many m³ of air will be in the tent?
- Four-sided 5917
 Mr. Radomír had a misfortune during the last storm; a tree fell on his roof in the shape of a regular four-sided pyramid and destroyed it all. The roof has a base edge length of 8m and a side edge length of 15m. How many m² of roofing will he have to buy?
Mr. Radomír had a misfortune during the last storm; a tree fell on his roof in the shape of a regular four-sided pyramid and destroyed it all. The roof has a base edge length of 8m and a side edge length of 15m. How many m² of roofing will he have to buy? - Quadrilateral 22003
 The shelter has the shape of a regular quadrilateral pyramid without a front wall. The length of the base edge is 3 meters, and the shelter's height is 3.5 meters. How much canvas must be bought to sew it if we have to increase consumption by 20% for fold
The shelter has the shape of a regular quadrilateral pyramid without a front wall. The length of the base edge is 3 meters, and the shelter's height is 3.5 meters. How much canvas must be bought to sew it if we have to increase consumption by 20% for fold - Roof cover
 Above the pavilion with a square ground plan with a side length of a = 12 m is a pyramid-shaped roof with a height v = 4.5 m. Calculate how much m² of sheet metal is needed to cover this roof; if 5.5% of the sheet, we must add for joints and waste.
Above the pavilion with a square ground plan with a side length of a = 12 m is a pyramid-shaped roof with a height v = 4.5 m. Calculate how much m² of sheet metal is needed to cover this roof; if 5.5% of the sheet, we must add for joints and waste. - Four-sided 19133
 The children's tent with a beech wood floor has the shape of a regular four-sided pyramid with a base edge of 1.25 m and a height of 80 cm. How much m² of fabric do we need to finish the tent if we add 12% material to the folds?
The children's tent with a beech wood floor has the shape of a regular four-sided pyramid with a base edge of 1.25 m and a height of 80 cm. How much m² of fabric do we need to finish the tent if we add 12% material to the folds? - Cross-section 62964
 The owner must cover the carport with a hipped roof with a rectangular cross-section of 8 m x 5 m. All roof surfaces have the same slope of 30°. Determine the price and weight of the roof if 1 m² cost €270 and weighs 43 kg.
The owner must cover the carport with a hipped roof with a rectangular cross-section of 8 m x 5 m. All roof surfaces have the same slope of 30°. Determine the price and weight of the roof if 1 m² cost €270 and weighs 43 kg.
- Quadrilateral pyramid
 The height of a regular quadrilateral pyramid is 6.5 cm, and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body—round calculations to 1 decimal place.
The height of a regular quadrilateral pyramid is 6.5 cm, and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body—round calculations to 1 decimal place. - Perimeter 83259
 The perimeter of the four-sided needle is 48 m, and its height is 2.5 m; how much will the sheet metal for this pyramid cost? If 1m² costs €1.5, a 12% loss due to joints and folds is included in the area.
The perimeter of the four-sided needle is 48 m, and its height is 2.5 m; how much will the sheet metal for this pyramid cost? If 1m² costs €1.5, a 12% loss due to joints and folds is included in the area. - Four-sided 15613
 The turret has the shape of a regular four-sided pyramid with a base edge 0.8 m long. The height of the turret is 1.2 m. How many square meters are needed to cover it, counting the extra 10% sheet metal waste?
The turret has the shape of a regular four-sided pyramid with a base edge 0.8 m long. The height of the turret is 1.2 m. How many square meters are needed to cover it, counting the extra 10% sheet metal waste? - Four-sided 5957
 How much m² of the galvanized sheet is used to cover the roof of the tower, which has the shape of a four-sided pyramid, whose base edge is 6 m long? The height of the tower is 9m. When covering, is 5% metal waste expected?
How much m² of the galvanized sheet is used to cover the roof of the tower, which has the shape of a four-sided pyramid, whose base edge is 6 m long? The height of the tower is 9m. When covering, is 5% metal waste expected? - Coverage 71484
 The tower's roof is a regular 4-sided pyramid with a height of 4m and an edge of the base of 6m. 25% of the roof covering was found to be damaged. How many square meters of coverage are needed to repair the roof?
The tower's roof is a regular 4-sided pyramid with a height of 4m and an edge of the base of 6m. 25% of the roof covering was found to be damaged. How many square meters of coverage are needed to repair the roof?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
