Line - practice problems - page 5 of 29
Number of problems found: 574
- Determine 82394
Determine the equation of the circle that passes through the point M(-1,2) and N( 3,0) and whose center lies on the line p: x=-3+t, y=-1+t, - Hypotenuse - construct problem
A line segment AA1 of length 6 cm is given. Construct all triangles ABC for which AA1 is the hypotenuse, side length BC is 5 cm, and angle gamma is 60°. - Calculate 82286
If I reduce a segment of length 72 cm in a ratio of 5:8, it will have a length of x cm. Calculate x. - Segment 82178
If I reduce a segment of length 72 cm in a ratio of 5:8, how many cm will it be? - Snowman's 82155
Under the column, the children built a 1.65m tall snowman. The snowman's shadow is 135 cm long. The shadow of the column has a length of 4.05 m. How tall is the pole? - Parametric 82072
Convert the parametric expression of the straight line to a general equation. x=3-5t y=-4+10t - Closest point
On the line p: 2x + y + 1 = 0, find the point A ∈ p that is closest to the point P =(1,0)
- Construction: 81894
Construct a rhombus that has a side length of 5 cm and a height of 4.5 cm. Outline: Analysis: Construction: Method: - Classroom 81784
The classroom is 6.8 m wide. Determine its width on a 1:50 scale plan. - X-coordinate 81737 In triangle ABC, determine the coordinates of point B if you know that points A and B lie on the line 3x-y-5=0, points A and C lie on line 2x+3y+4=0, point C lies on the x-coordinate axis, and the angle at vertex C is right.
- Coefficient 81704
In the equation of the line p: ax-2y+1=0, determine the coefficient a so that the line p: a) it formed an angle of 120° with the positive direction of the x-axis, b) passed through point A[3,-2], c) was parallel to the x-axis, d) had a direction of k = 4. - Probability 81637
We randomly select three different points from the vertices of a regular heptagon and connect them with line segments. The probability that the resulting triangle will be isosceles is equal to: (A) 1/3 (B) 2/5 (C) 3/5 (D) 4/7 - In plane 2 A triangle ABC is located in the plane with a right angle at vertex C, for which the following holds: A(1, 2), B(5, 2), C(x, x+1), where x > -1. a) determine the value of x b) determine the coordinates of point M, which is the midpoint of line segment
- Intersection 81611
Given a triangle ABC: A (-1,3), B(2,-2), C(-4,-3). Determine the coordinates of the intersection of the heights and the coordinates of the intersection of the axes of the sides. - Quadrilateral calc
The square ABCD is given. The midpoint of AB is E, the midpoint of BC is F, CD is G, and the midpoint of DA is H. Join AF, BG, CH, and DE. Inside the square (approximately in the middle), the intersections of these line segments form a quadrilateral. Calc
- Advantageous 81389
The room has dimensions of 11 m x 5 m. Lino will be purchased for the room, which is sold in a roll with a width of 2 meters. How many meters of rope will be needed, and how much will be left? Consider both options for laying the line (lengthwise and widt - Gradient of the railway
Calculate the gradient of the railway line, which has an elevation of 22.5 meters in a section of 1.5 kilometers. For railways, the result is given in h (per mille). - Respectively 81293
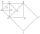The figure shows the squares ABCD, EFCA, CHCE, and IJHE. Points S, B, F, and G are, respectively, the centers of these squares. Line segment AC is 1 cm long. Determine the area of triangle IJS. Please help... - Intersection 81017
There are also two equilateral triangles ABC, and BDE, such that the size of the angle ABD is greater than 120° and less than 180° points C and E lie in the same half-plane defined by the line AD. The intersection of CD and AE is marked F. Determine the s - Respectively 80982
The vertices of the square ABCD are joined by the broken line DEFGHB. The smaller angles at the vertices E, F, G, and H are right angles, and the line segments DE, EF, FG, GH, and HB measure 6 cm, 4 cm, 4 cm, 1 cm, and 2 cm, respectively. Determine the ar
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
