Heptagon triangle probability

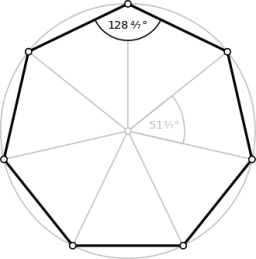
We randomly select three different points from the vertices of a regular heptagon and connect them with line segments. The probability that the resulting triangle will be isosceles is equal to:
(A) 1/3
(B) 2/5
(C) 3/5
(D) 4/7

Final Answer:

p =  3/5

Step-by-step explanation:

$$\begin{gathered} n=7 \\ p=\frac{7\cdot 6\cdot 3}{7\cdot 6\cdot 5}=\frac{3}{5}=0.6 \end{gathered}$$

Try another example