Modulo - practice problems
The modulo operation finds the remainder after division of one number by another, denoted as a mod n or a % n. For example, 17 mod 5 = 2 because 17 divided by 5 gives 3 with remainder 2. Modular arithmetic treats numbers as equivalent if they differ by a multiple of the modulus, creating a cyclical number system. This concept is fundamental to number theory, cryptography, and computer science. Applications include determining odd/even numbers, clock arithmetic, check digit algorithms, and hash functions. The modulo operation has unique properties and forms the basis of modular arithmetic used in advanced mathematics and digital security systems.Instructions: Solve each problem carefully and provide a detailed solution for every item.
Number of problems found: 25
- A labourer
A laborer who works five days a week starts at 10 AM on Monday. If he works for 56 days, on which day will he complete the job? - Market open A certain market opens for sales every 7th day of the week. If it opened last on a Friday, what day of the week will the market be opened again after nine months? (Hint: a month is 30 days)
- Fraction to decimal infinite
Find which digit is at 1000th place after the decimal point in the decimal expansion of the fraction 9/28. - Quarter of an hour
If the clock showed a quarter of an hour more, it would be 10 minutes to 10 hours. How many hours do they show? - Factorial division remainder
Find the remainder after division when we divide the sum of 1! +2! +3! +. ... . +300! number 13. - Day week calculation
If the day before yesterday was the day of the week, what day of the week would it be from today in 50 days? (0 = Monday, 6 = Sunday) - Twos
Vojta started writing the number this year, 2019202020192020, into the workbook. And so he kept going. When he wrote 2020 digits, he no longer enjoyed it. How many twos did he write? - Number divisor proof
The natural number n has at least 73 two-digit divisors. Prove that one of them is the number 60. Also, give an example of the number n, which has exactly 73 double-digit divisors, including a proper justification. - Hexagonal pattern
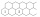The figure shows two rows of hexagonal boxes that continue to the right without restriction. Fill in one field with one positive integer so that the product of the numbers in any three adjacent fields is 2018. Determine the number that will be in the top - Middle finger
Jana counts on one hand one by one. She starts counting from her thumb through her index finger, middle finger, and ring finger and comes to her little finger and has the number 5. Then she immediately returns to her ring finger (6), to her middle finger - Electricity blackout
On Tuesday at 6 o'clock, the electricity supply was interrupted at 156 h. On which day (1 = Monday, ... 7 = Sunday) and at what time was the electricity supply resumed? - Big number
What is the remainder when dividing 10 by 9 to 47 - 111? - Christmas
Father said, " Exactly after 56 hours, we will sit down at the Christmas Eve table." How was it, and what time was it, when Father said this sentence? They sat at the Christmas Eve table at exactly 6 PM. - Modulo Find x in the modulo equation: 47x = 4 (mod 9) Hint - read as what number 47x divided by 9 (modulo 9) gives remainder 4.
- Sheep arrangement
Shepherd has less than 500 sheep. If he organizes them in 4 rows, he will remain three sheep. If he manages them in 5 rows, he will remain four sheep. If he arranges them in 6 rows, he will remain five sheep. But it can manage them exactly in 7 rows. How - Grandmother's clocks
Grandmother's clock is half a minute late every hour. Grandmother set the clock exactly at 8.00 AM. How many hours will show after 24 hours? - Clock hands
The hands-on clock shows the time as 12 hours and 2 minutes. Three hours later, calculate the size of an acute angle between the clock hands. - Christmas
Exactly after 114 hours, we sit down at the Christmas Eve table. What day and what time was it when Dad said this sentence? They sit at the Christmas Eve table exactly at the 18-o'clock (6 PM). - Remainders
It is given a set of numbers { 200; 261; 331; 345; 487; 554 }. Divide these numbers by number 80 and determine a set of remainders. As a result, write the sum of these remainders. - Sweets
Mom bought a box of sweets for their children. The whole package of 102 sweets is divided among 3 their children so that each child receives the most and she remains the least sweets. How many sweets are left for Mom?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
