Restriction 7442
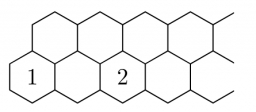
The figure shows two rows of hexagonal boxes that continue to the right without restriction. Fill in one field with one positive integer so that the product of the numbers in any three adjacent fields is 2018. Determine the number that will be in the top row in the 2019 field.
Correct answer:
Tips for related online calculators
Do you want to perform natural numbers division - find the quotient and remainder?
You need to know the following knowledge to solve this word math problem:
algebraarithmeticbasic operations and conceptsnumbersthemes, topicsGrade of the word problem
Related math problems and questions:
- Z9–I–1
All nine fields of given shape are to be filled with natural numbers so that: • each of the numbers 2, 4, 6, and 8 is used at least once, • four of the inner square boxes containing the products of the numbers of adjacent cells of the outer square, • in t - Cans
How many cans must be put in the bottom row if we want 182 cans arranged in 13 rows above so that each subsequent row has always been one in less? How many cans will be in the top row? - MO Z6-6-1
Write integers greater than 1 to the blanks in the following figure so that each darker box is a product of the numbers in the neighboring lighter boxes. What number is in the middlebox? - Year 2018
The product of the three positive numbers is 2018. What are the numbers? - Negative integer
What will be the sign of the product if you multiply eight negative integers with one positive integer? - Chad buys
Chad buys peanuts in 2-pound bags. He repackages them into bags that hold 5/6 pounds of peanuts. How many 2-pound bags of peanuts should Chad buy to fill the 5/6-pound bags without having any peanuts left over? - Cat show
A total of ten exhibitors gathered at the long-haired cat show. It was exhibited in a rectangular room with two rows of tables, as shown. The cats were marked with different numbers from 1 to 10, and one cat sat on each table. Determine which cat was rate
