Year 2018
The product of the three positive numbers is 2018. What are the numbers?
Correct answer:
Tips for related online calculators
Do you solve Diofant problems and are looking for a calculator of Diofant integer equations?
Do you want to convert time units like minutes to seconds?
Do you want to convert time units like minutes to seconds?
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Themes, topics:
Related math problems and questions:
- Restriction 7442
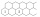The figure shows two rows of hexagonal boxes that continue to the right without restriction. Fill in one field with one positive integer so that the product of the numbers in any three adjacent fields is 2018. Determine the number that will be in the top - When three
When three positive integers a, b, and c are multiplied together, their product is 64. Suppose a < b < c. In how many ways can the numbers be chosen? - MO Z8-I-1 2018
Fero and David meet daily in the elevator. One morning, they found that if they multiply their current age, they get 238. If they did the same after four years, this product would be 378. Determine the sum of the current ages of Fero and David. - The product 4
The product of two simple fractions is 12/35. If one of the fractions is 3/7, what is the other one?
- Function
For linear function f(x) = ax + b is f(19)=141; f(20)=168. Calculate m, if f(m) = 2018. - Divisible 67434
The number of Beata's house is 2018. The numbers of Jura's and Dan's houses are made up of the same numbers. A) What number of Jura's house can be if it is divisible by 4? List all the options. B) What can Dan's house number be if it is divisible by 5? Li - The product 18
The product of two consecutive natural numbers which are multiples of 3 is equal to 810. Find the two numbers.
