MO Z6–I–3 2018
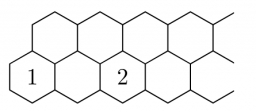
Na obrázku sú naznačené dva rady šesťuholníkových políčok, ktoré doprava pokračujú bez obmedzenia. Do každého políčka doplňte jedno kladné celé číslo tak, aby súčin čísel v ľubovoľných troch navzájom susediacich políčkach bol 2018. Určte číslo, ktoré bude v 2019-tom políčku v hornom rade.
Vaša odpoveď:
Vaša odpoveď:
Zobrazujem 4 komentáre:
Žiak
videl som tuto ulohu na papiery ... zo zadania my nebolo jasne ze susediace mozu byt len policka v ramci jedneho riadku ...
Tipy na súvisiace online kalkulačky
Chcete previesť delenie prirodzených čísel - zistiť podiel a zvyšok?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebraaritmetikazákladné operácie a pojmyčíslatémaÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- MO Z6-6-1
Do prázdnych polí v nasledujúcom obrázku doplňte celé čísla väčšie ako 1 tak, aby v každom tmavšom políčku bol súčin čísel zo susedných svetlejších políčok: Aké je číslo je v strede? - Rok 2018
Súčin troch kladných čísel je 2018. Ktoré sú to čísla? - Máme vytvoriť
Máme vytvoriť políčko v tvare obdĺžnika s rozlohou 288 m² (štvorcových), tak aby strany boli celé čísla. Aké sú všetky rozmery obdĺžnikového políčka, ktoré môžeme vytvoriť? Koľko je riešení. - Šachovnica 2
Určte, koľkými spôsobmi môžeme na šachovnici 8x8 postaviť 5 rôznych figúrok tak, aby dve stáli na čiernych a tri na bielych políčkach? - Obdĺžnik - kto má pravdu
Obdĺžnik je rozdelený na 7 políčok. Na každé políčko sa má napísať práve jedno z čísel 1, 2 a 3. Mirek tvrdia, že to možno vykonať tak, aby súčet dvoch vedľa seba napísaných čísel bol zakaždým iný. Zuzka naopak tvrdia, že to možné nie je. Rozhodnite, kto - Richardove čísla Z8-I-2 2019
Richard sa pohrával s dvoma päťcifernými číslami. Každé pozostávalo z navzájom rôznych cifier, ktoré pri jednom boli všetky nepárne a pri druhom všetky párne. Po chvíli zistil, že súčet týchto dvoch čísel začína dvojčíslím 11 a končí číslom 1 a že ich roz - Z7–I–6, výstava mačiek
Na výstave dlhosrstých mačiek sa zišlo celkom desať vystavujúcich. Vystavovalo sa v obdĺžnikovej miestnosti, v ktorej boli dva rady stolov ako na obrázku. Mačky boli označené navzájom rôznymi číslami v rozmedzí 1 až 10 a na každom stole sedela jedna mačka
