Pythagoras contest - practice problems - page 2 of 3
Direction: Solve each problem carefully and show your solution in each item.Number of problems found: 58
- Distribute 70244
We have to distribute the keys to the safe among four people so that no two of them can open the safe but in such a way that any three can open the safe. How many minimum keys do we need? How to divide them? How many minimum locks must be on the safe? All - Beginning 66104
The kangaroo always jumps three steps up. Each time he jumps, the bunny jumps down two steps. On which stairs will they meet? The kangaroo stands on the 1st step at the beginning and the bunny on the 100th. - Grandma
Grandma is 57 years older than her two twin granddaughters. If we add the ages of an older woman with both granddaughters, we get the number 99. How old is her old woman? - The number - digits
The vortex of the three given digits formed different three-digit numbers. When she added up all these numbers, she published 1554. What numbers did Vierka use?
- Different 55491
Add the same numbers after the same letters and different numbers after the other letters so that equality applies: KRAVA + KRAVA = MLIEKO, where K is an odd digit. - Four-digit 55481
Find all four-digit abcd numbers to which abcd = 20. ab + 16. cd, where ab and cd are double digits numbers from digits a, b, c, and d. - The isosceles
The isosceles trapezoid ABCD has bases of 18 cm and 12 cm. The angle at apex A is 60°. What is the circumference and area of the trapezoid? - Phone number
Ivan's phone number ends with a four-digit number: When we subtract the first from the fourth digit of this four-digit number, we get the same number as when we subtract the second from the third digit. If we write the four-digit number from the back and - Five-digit number
Anna thinks of a five-digit number not divisible by three or four. If he increments each digit by one, it gets a five-digit number divisible by three. If he reduces each digit by one, he gets a five-digit number divisible by four. If it swaps any two digi
- All pairs
Find all pairs (m, n) of natural numbers for which is true: m s (n) = n s (m) = 70, where s(a) denotes the digit sum of the natural number a. - Census pyramid
Vojta added five different prime numbers to the top row of the census pyramid. Their sum was 50. What was the biggest number he could get "down"? - Candles
Before Christmas, Eva bought two cylindrical candles—red and green. Red was 1 cm longer than green. She lit a red candle on Christmas Day at 5:30 PM and a green candle at 7:00 PM, leaving them on fire until they burned. At 9:30 PM, both candles were the s - Yesterday 13711
If the day before yesterday was the day of the week, what day of the week would it be from today in 50 days? (0 = Monday, 6 = Sunday) - Apples and pears
Apples cost 50 cents a piece, pears 60 cents a piece, bananas cheaper than pears. Grandma bought five pieces of fruit. There was only one banana, and I paid 2 euros 75 cents. How many apples and how many pears?
- Two cars on ring
Two cars were on the round track (ring) in the adjacent tracks, the first on the inner track and the second on the outer track. Both cars started at the same time from one starting track. The first toy car drove four laps simultaneously, and the second to - Self-counting machine
The self-counting machine works exactly like a calculator. The innkeeper wanted to add several three-digit natural numbers on his own. On the first attempt, he got the result in 2224. To check, he added these numbers again, and he got 2198. Therefore, he - Equilateral triangle ABC
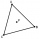In the equilateral triangle ABC, K is the center of the AB side, the L point lies on one-third of the BC side near point C, and point M lies on one-third of the side of the AC side closer to point A. Find what part of the ABC triangle contains the triangl - Special watch
Fero bought a special watch on the market. It has only one (minute) hand and a display showing the angle between the hour and minute hands. How many hours was his watch shown? The minute hand points to number 2; the display shows 125°. - Two rectangles
I cut out two rectangles with 54 cm² and 90 cm². Their sides are expressed in whole centimeters. If I put these rectangles together, I get a rectangle with an area of 144 cm². What dimensions can this large rectangle have? Write all options. Explain your
Three years ago, the triplets Pavel, Petr, Luke, and their five-year-old sister Jane had been together for 25 years. How old is Jane today?Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
