Self-counting machine
The self-counting machine works exactly like a calculator. The innkeeper wanted to add several three-digit natural numbers on his own. On the first attempt, he got the result in 2224. To check, he added these numbers again, and he got 2198. Therefore, he added these numbers again, and now he got the sum of 2204. He always entered the fifth added number incorrectly because he needed to press its digits harder on each attempt. In the self-calculation, he always entered a two-digit number instead of a three-digit number. He did not make any other errors in the census; this time, the self-count also worked flawlessly. What is the correct sum of inn numbers?
Correct answer:
Tips for related online calculators
Do you have a system of equations and are looking for calculator system of linear equations?
Do you solve Diofant problems and are looking for a calculator of Diofant integer equations?
Do you solve Diofant problems and are looking for a calculator of Diofant integer equations?
You need to know the following knowledge to solve this word math problem:
algebraarithmeticbasic operations and conceptsnumbersthemes, topicsGrade of the word problem
Related math problems and questions:
- Double-digit 80970
Eva thought of two natural numbers. She first added these correctly, then subtracted them correctly. In both cases, she got a double-digit result. The product of the resulting two-digit numbers was 645. Which numbers did Eva think of? Please, what is this - Phone numbers
How many 9-digit telephone numbers can be compiled from the digits 0,1,2,..,8,9 that no digit is repeated? - Odd/even number
Pick any number. If that number is even, divide it by 2. If it's odd, multiply it by three and add one. Now, repeat the process with your new number. If you keep going, you'll eventually end up at one every time. Prove. - Mistake
Nicol needs to correct errors when calculating in school. Instead of adding the number 20, she subtracts it. What is the difference between the result and the correct result?
- Mathematicians 11761
The top five mathematicians in the class took on the teacher's help in calculating the paper's average grade. They dictated the following results: Mischa: "I came up with 3.30. " Dasha: "That's weird because it worked out precisely at 3.45. " Jana: "You p - Beta's number
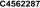Beta thought of a natural number with different digits and wrote it on the board. Below wrote the digits of the original number on the back and thus got a new number. By adding these two numbers, he got a number with the same number of digits as the inten - Four-digit 10261
Roman likes magic and math. Last time he conjured three- or four-digit numbers like this: • created two new numbers from the given number by dividing it between digits in the place of hundreds and tens (e.g., from the number 581, he would get 5 and 81), •
