Volume - practice problems - page 2 of 126
Volume is always the third power of length. Or volume = area times length. For example, the volume of the cube is a3, and the prism's volume is S*h (the area of the base times the height). The volume of rotating bodies (sphere, cone) can be derived in high school by integration. The pyramid's volume is always 1/3 of the prism's volume. We calculate the volume of the truncated bodies either with a formula or simply by subtracting the volumes of the two bodies.Number of problems found: 2516
- Gas tank
 Mason's car has a gas tank that holds 24 gallons of gas. The tank is precisely 1/4 full. How many gallons of gas are in Mason's car?
Mason's car has a gas tank that holds 24 gallons of gas. The tank is precisely 1/4 full. How many gallons of gas are in Mason's car? - A solution 2
 To a solution of 30 litres containing 90% alcohol, how much water must be added to so that the alcohol becomes 80%?
To a solution of 30 litres containing 90% alcohol, how much water must be added to so that the alcohol becomes 80%? - Revolving to cone
 A triangle whose sides are 20 cm, 16 cm, and 12 cm is revolving around its greatest side as axis. What is the volume space it generates after a full revolution in cubic centimeters?
A triangle whose sides are 20 cm, 16 cm, and 12 cm is revolving around its greatest side as axis. What is the volume space it generates after a full revolution in cubic centimeters? - A tank 3
 A tank is 3/5 full of water. 50 liters more of water is required to fill the tank, how many liters of water can the tank hold?
A tank is 3/5 full of water. 50 liters more of water is required to fill the tank, how many liters of water can the tank hold? - Milk bottles
 A container of milk was 4/5 full. When 12 bottles of milk were taken out and 8 bottles of milk poured into it, it was 3/4 full.How many bottles of milk can the container contain?
A container of milk was 4/5 full. When 12 bottles of milk were taken out and 8 bottles of milk poured into it, it was 3/4 full.How many bottles of milk can the container contain? - Full-tank
 A full-tank of petrol a car lasts for 10 days. If driver starts using 25% more everyday, how many days will the full-tank petrol last?
A full-tank of petrol a car lasts for 10 days. If driver starts using 25% more everyday, how many days will the full-tank petrol last? - The dimensions
 The dimensions of a rectangular piece of paper are 22 cm × 14 cm. It is rolled once across the breadth and once across the length to form right circular cylinders of biggest possible surface area. Find the difference in volumes of the two cylinders that w
The dimensions of a rectangular piece of paper are 22 cm × 14 cm. It is rolled once across the breadth and once across the length to form right circular cylinders of biggest possible surface area. Find the difference in volumes of the two cylinders that w - Spheres to cone
 Two solid spheres of radii 2 cm and 4 cm are melted and recast into a cone of height 8 cm. Find the radius of the cone so formed.
Two solid spheres of radii 2 cm and 4 cm are melted and recast into a cone of height 8 cm. Find the radius of the cone so formed. - Ones cube
 Find the volume of a cube whose total surface area is 6 m².
Find the volume of a cube whose total surface area is 6 m². - A random 2
 A random sample of 40 families has an average water consumption of 29 cubic meters per month, with a sample standard deviation of 8 cubic meters. Give the 90% confidence interval for the mean usage of water per month.
A random sample of 40 families has an average water consumption of 29 cubic meters per month, with a sample standard deviation of 8 cubic meters. Give the 90% confidence interval for the mean usage of water per month. - A tank 2
 A tank can be filled by a pipe A in 3 hours and by pipe B in 5 hours. When the tank is full, it can be drained by pipe C in 4 hours. If the tank is initially empty and all three pipes are open, how many hours will it take to fill up the tank?
A tank can be filled by a pipe A in 3 hours and by pipe B in 5 hours. When the tank is full, it can be drained by pipe C in 4 hours. If the tank is initially empty and all three pipes are open, how many hours will it take to fill up the tank? - A bottle 3
 A bottle of water contains 16.9 ounces. How many total ounces are there in 24 bottles?
A bottle of water contains 16.9 ounces. How many total ounces are there in 24 bottles? - The petrol tank
 Tinny's car's petrol tank was full. He drove around the city and used 1/4 of the petrol. What fraction of the petrol was left?
Tinny's car's petrol tank was full. He drove around the city and used 1/4 of the petrol. What fraction of the petrol was left? - Full tank 2
 Robert has a full tank of petrol. He drove to Manly and used 1/8 of a tank and then to Gosford using another 4/8 of a tank. What fraction of a tank of petrol has he used?
Robert has a full tank of petrol. He drove to Manly and used 1/8 of a tank and then to Gosford using another 4/8 of a tank. What fraction of a tank of petrol has he used? - The cuboid 2
 If the areas of three adjacent faces of a cuboid are 6,10,22 respectively then find the volume of the cuboid.
If the areas of three adjacent faces of a cuboid are 6,10,22 respectively then find the volume of the cuboid. - The frustum
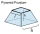 A frustum of a pyramid is 4 cm at the top and 7 cm at the bottom square, and it's 6 cm high. Calculate the volume of the frustum.
A frustum of a pyramid is 4 cm at the top and 7 cm at the bottom square, and it's 6 cm high. Calculate the volume of the frustum. - A swimming 2
 A swimming pool had 2.5 million liters of water in it. Some water evaporated, and then the pool only had 2 million liters of water in it. What percent of the water evaporated?
A swimming pool had 2.5 million liters of water in it. Some water evaporated, and then the pool only had 2 million liters of water in it. What percent of the water evaporated? - Milk mixture
 In a container, milk and water are 7:5. If 15 L water is added, the ratio becomes 7:8. Find the quantity of water in the new mixture.
In a container, milk and water are 7:5. If 15 L water is added, the ratio becomes 7:8. Find the quantity of water in the new mixture. - Two pipes 3
 Two pipes, A and B, can fill a tank in 15 minutes and 20 minutes, respectively. Both pipes are opened together. After 4 minutes, pipe A is turned off.What is the total time required to fill the tank?
Two pipes, A and B, can fill a tank in 15 minutes and 20 minutes, respectively. Both pipes are opened together. After 4 minutes, pipe A is turned off.What is the total time required to fill the tank? - A conical
 A conical tent can accommodate 11 people. Each person needs 4 m² of space on the ground and 20 m³ of air to breathe. Find the height of the tent.
A conical tent can accommodate 11 people. Each person needs 4 m² of space on the ground and 20 m³ of air to breathe. Find the height of the tent.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
