Spheres to cone
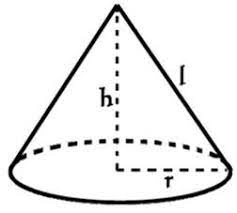
Two solid spheres of radii 2 cm and 4 cm are melted and recast into a cone of height 8 cm. Find the radius of the cone so formed.
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticsolid geometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Cylinder-shaped part
A truncated cone-shaped part with base radii of 4 cm and 22 cm is to be recast into a cylinder-shaped part of the same height as the original part. What base radius will the new part have? - Three cubes
Three cubes of iron whose edges are 6 cm, 8 cm, and 10 cm, respectively, are melted and formed into a single cube. Find the edge of the new cube. - A solid
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid . - Without 8260
The ice cream sundae glass has a cone shape. Its height without legs is 9 cm, and its radius is 5 cm. Šimon bought eight scoops of ice cream, which all melted in the sun. One scoop of ice cream has a volume of 32 cm³. How many cm³ of melted ice cream will
- Frustrum - volume, area
Calculate the surface and volume of a truncated rotating cone with base radii of 8 cm and 4 cm and a height of 5 cm. - Ratio
The radii of the two cones are in the ratio of 5.7. Calculate the area ratio of cones that have the same height. - Volume of the cone
Find the volume of the cone with the base radius r and the height v. a) r = 6 cm, v = 8 cm b) r = 0,9 m, v = 2,3 m c) r = 1,4 dm, v = 30 dm
