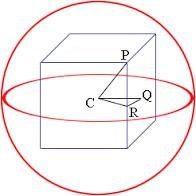
Cube in sphere
The sphere is an inscribed cube with an edge of 8 cm. Find the sphere's radius.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Sphere area
A cube with an edge 1 m long is a circumscribed sphere (vertices of the cube lie on a sphere's surface). Find the surface area of the sphere. - Inscribed circle
A circle is inscribed at the bottom wall of the cube with an edge (a = 1). What is the radius of the spherical surface that contains this circle and one of the vertex of the top cube base? - Inscribed
The cube is inscribed in the cube. Determine its volume if the edge of the cube is 10 cm long. - Spheres in sphere
How many spheres with a radius of 15 cm can fit into the larger sphere with a radius of 150 cm?
- Percentage 3481
We turned a sphere with the largest possible radius from a cube with an edge length of 8 cm. Calculate the volume of the cube, the ball, and the percentage of waste when turning. - Inscribed 81949
A cube is inscribed in a sphere with a radius of 27 cm. Calculate its volume and surface area. - Cube in sphere
The cube is inscribed in a sphere with a radius r = 6 cm. What percentage is the cube's volume from the ball's volume?
