Tangent spheres
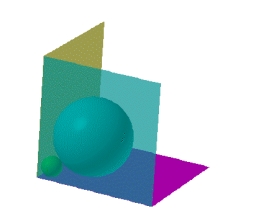
A sphere with a radius of 1 m is placed in the corner of the room. What is the largest sphere size that fits into the corner behind it?
Additional info: Two spheres are placed in a corner of a room. The spheres are each tangent to the walls and floor and tangent to each other.
Additional info: Two spheres are placed in a corner of a room. The spheres are each tangent to the walls and floor and tangent to each other.
Correct answer:
Tips for related online calculators
The Pythagorean theorem is the base for the right triangle calculator.
See also our trigonometric triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Billiard balls
A layer of ivory billiard balls of radius 6.35 cm is in the form of a square. The balls are arranged so that each ball is tangent to every one adjacent to it. In the spaces between sets of 4 adjacent balls other balls rest, equal in size to the original. - Spheres in sphere
How many spheres with a radius of 15 cm can fit into the larger sphere with a radius of 150 cm? - Percentage 39373
Inside the 10 cm cube, a sphere is placed so that it touches all the cube's walls. What percentage of the volume of a cube makes up the volume of a sphere? - On the floor 2
The floor area of a living room is 9 7/9 m². A carpet with an area of 5 5/8 m² is placed on the floor. Find the area of the room that is not covered with carpet. - Metal balls
Four metal balls with a diameter of 5 cm are placed in a measuring cylinder with an inner diameter of 10 cm. What is the smallest water volume to be poured into the cylinder so that all balls are below the water level? - Two balls
Two balls, one 8cm in radius and the other 6cm in radius, are placed in a cylindrical plastic container 10cm in radius. Find the volume of water necessary to cover them. - Cannonballs
Of the three cannonballs with a diameter of 16 cm, which landed in the castle courtyard during the battle, the castle blacksmith cast balls with a diameter of 10 cm, which fit into the cannons placed on the walls. How many cannonballs did the blacksmith c - Rectangular 2885
A total of ten exhibitors gathered at the long-haired cat show. It was exhibited in a rectangular room with two rows of tables as shown. The cats were marked with different numbers from 1 to 10, and one cat sat on each table. Determine which cat was rated - Sphere and cone
Within the sphere of radius G = 33 cm inscribe the cone with the largest volume. What is that volume, and what are the dimensions of the cone? - Chauncey
Chauncey is building a storage bench for his son’s playroom. The storage bench will fit into the corner and against two walls to form a triangle. Chanuncy wants to buy a triangular shaped cover for the bench. If the storage bench is 2 1/2 ft. Along one wa - Cube in sphere
The sphere is an inscribed cube with an edge of 8 cm. Find the sphere's radius. - Tiles
The room has dimensions 12 m and 5.6 m. Determine the number of square tiles and their largest possible size to cover them room's floor. - Surveyors
Surveyors mark 4 points on the surface of the globe so that their distances are the same. What is their distance from each other? - Sports students
There are 120 athletes, 48 volleyball players, and 72 handball players at the school with extended sports training. Is it possible to divide sports students into groups so that the number in each group is the same and expressed by the largest possible num - Laths
There are two laths in the garage opposite one another: one 2 meters long and the other 3 meters long. They fall against each other and lean against the opposite walls of the garage both laths and touch at a height of 70 cm above the garage floor. How wid - Cube from sphere
What largest surface area (in cm²) can have a cube that we cut out of a sphere with radius 43 cm? - Highest 62464
The iron pipes are placed in 10 rows, one above the other so that in the highest upper row, there are 15 pipes, and in each other, there is one tube more. How many pipes are there?
