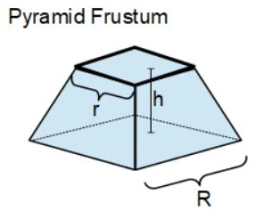
The frustum
A frustum of a pyramid is 4 cm at the top and 7 cm at the bottom square, and it's 6 cm high. Calculate the volume of the frustum.
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
arithmeticsolid geometryplanimetricsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- A frustum
A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume. - Hexagon cut pyramid
Calculate the volume of a regular 6-sided cut pyramid if the bottom edge is 30 cm, the top edge is 12 cm, and the side edge length is 41 cm. - Quadrangular pyramid
Calculate the surface area and volume of a regular quadrangular pyramid: sides of bases (bottom, top): a1 = 18 cm, a2 = 6cm angle α = 60 ° (Angle α is the angle between the sidewall and the base plane.) S =? , V =? - Quadrilateral 81033
The foundations of a regular truncated quadrilateral pyramid are squares. The lengths of the sides differ by 6 dm. Body height is 7 dm. The body volume is 1813 dm³. Calculate the lengths of the edges of both bases. - Pit
The pit is 1.2 m deep and in the shape of a truncated pyramid with a rectangular base. Its length and width are the top 3 × 1.5 m and the bottom 1 m × 0.5 m. To paint one square meter of the pit, we use 0.8 l of green paint. How many liters of paint are n - 4B - truncated pyramid
Calculate the volume of a regular truncated quadrilateral pyramid if the base edges are 10cm and 4cm and the height of the side wall is 5cm. - Truncated pyramid
The truncated regular quadrilateral pyramid has a volume of 74 cm3, a height v = 6 cm, and an area of the lower base 15 cm² greater than the upper base's area. Calculate the area of the upper base.
