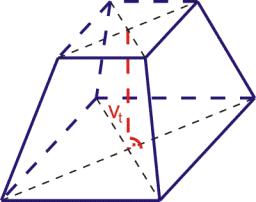
Quadrangular pyramid
Calculate the surface area and volume of a regular quadrilateral pyramid:
sides of bases (bottom, top): a1 = 18 cm, a2 = 6 cm
angle α = 60 ° (Angle α is the angle between the sidewall and the base plane.)
S =? , V =?
Your answer:
sides of bases (bottom, top): a1 = 18 cm, a2 = 6 cm
angle α = 60 ° (Angle α is the angle between the sidewall and the base plane.)
S =? , V =?
Your answer:
Tips for related online calculators
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Pyramid - angle
Calculate the regular quadrilateral pyramid's surface, the base edge of which is measured 6 cm, and the deviation from the plane of the base's sidewall plane is 50 degrees. - 4side pyramid
Calculate the volume and surface of the regular four-sided pyramid whose base edge is 4 cm long. The angle from the plane of the sidewall and base plane is 60 degrees. - Tetrahedral pyramid
Determine the surface of a regular tetrahedral pyramid when its volume is V = 120 and the angle of the sidewall with the base plane is α = 42° 30'. - Quadrilateral pyramid
A regular quadrilateral pyramid has a volume of 24 dm³ and a base edge a = 4 dm. Calculate: a/height of the pyramid b/sidewall height c/surface of the pyramid - Quadrilateral pyramid
The regular quadrilateral pyramid has a base edge a = 1.56 dm and a height h = 2.05 dm. Calculate: a) the deviation angle of the sidewall plane from the base plane b) deviation angle of the side edge from the plane of the base - Regular quadrangular pyramid
How many square meters are needed to cover a regular quadrilateral pyramid base edge of 10 meters if the deviation lateral edges from the base plane are 68°? Calculate waste 10%. - Tetrahedral pyramid
Calculate the regular tetrahedral pyramid's volume and surface if the area of the base is 20 cm² and the deviation angle of the side edges from the plane of the base is 60 degrees.
