Pit
The pit is 1.2 m deep and in the shape of a truncated pyramid with a rectangular base. Its length and width are the top 3 × 1.5 m and the bottom 1 m × 0.5 m. To paint one square meter of the pit, we use 0.8 l of green paint. How many liters of paint are needed when we paint only the sides and bottom of the pit?
Correct answer:
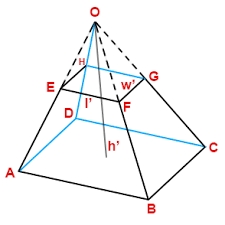
Showing 2 comments:
Math student
the process of the answer is not enough clear try to associate it well with the graph
Dr Math
yes, the image is only for illustration .... symbols have not the same meaning as in solutions... We re-write steps of solutions to be more clear.
Tips for related online calculators
Do you want to convert length units?
Tip: Our volume units converter will help you convert volume units.
The Pythagorean theorem is the base for the right triangle calculator.
Do you want to round the number?
Tip: Our volume units converter will help you convert volume units.
The Pythagorean theorem is the base for the right triangle calculator.
Do you want to round the number?
You need to know the following knowledge to solve this word math problem:
arithmeticsolid geometryplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Flowerpot
The block-shaped flowerpot has external dimensions: length 1.25 m, width 10 cm, and height 11 cm. The thickness of the boards from which it is made is 0.8 cm. How many liters of soil is needed to fill it 1 cm below the top edge? What surface do we have to - Truncated 43851
The pit is a regular truncated 4-sided pyramid, with 14 m and 10 m base edges and a depth of 6m. Calculate how much m³ of soil was removed when we dug this pit. - Wooden bowls
Twenty wooden bowls in the shape of a truncated cone should be painted on the outside and inside with wood varnish. We need 0.1 l of paint to paint 200 cm². How many liters of paint do we have to buy if the bowls are 25 cm high, the bottom of the bowl has - Digging a pit
The pit has the shape of a regular quadrilateral truncated pyramid. The edges of the bases are 14m and 10m long. The sidewalls form an angle of 135° with a smaller base. Find how many m³ of soil were excavated when digging the pit. - Pool
The prism-shaped pool is 2 m deep, with a bottom of the isosceles trapezoid, base dimensions of 10 m and 18 m, and arms legs 7 m long and 5.7 m long. During the spring cleaning, we must paint the bottom and walls of the pool. How many m² of paint should b - Rectangular 6481
The bottom of the pool at the family house has a rectangular shape with dimensions of 5 m and 3.5 m. Its height is 1.2 m. How many kg of acrylic paint are needed to paint the bottom and walls of the pool if 1 kg of paint is enough for 6 m²? The coating is - Concreted
The tank of a biological treatment plant has the shape of a cylinder with a base diameter of 2.5m. It is usually filled to four-fifths of its volume. What is the volume of the treatment plant if its height is 2.8m? The treatment plant container is placed
