n choose k calculator n=11, k=1 result

Find out how many different ways you can choose k items from n items set without repetition and without order. This number is also called combination number or n choose k or binomial coefficient or simply combinations. See also general combinatorial calculator.

Elements to choose from:

(n)

Elements chosen:

(k)

Calculate

A bit of theory - the foundation of combinatorics

Combinations

A combination of a k-th class of n elements is an unordered k-element group formed from a set of n elements. The elements are not repeated, and it does not matter the order of the group's elements. In mathematics, disordered groups are called sets and subsets. Their number is a combination number and is calculated as follows:

$C_k(n)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)=\frac{n!}{k!(n-k)!}$

A typical example of combinations is that we have 15 students and we have to choose three. How many will there be?

Foundation of combinatorics in word problems

• 7 heroes
  6 heroes galloping on 6 horses behind. How many ways can we sort them behind?
• MATES
  In MATES (Small Television tipping), from 35 random numbers, five winning numbers are drawn. How many possible combinations are there?
• Intersection of the lines
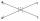  How many points do nine lines intersect in a plane, of which four are parallel, and of the other five, no two are parallel (and if we assume that only two lines pass through each intersection)?
• PIN - codes
  How many five-digit PIN - codes can we create using the even numbers?

• Probability 3219
  In recent years, it has rained 12 days in March. What is the probability that it rained on March 18?
• Three-digit code
  The five cards with the numbers 1, 2, 3, 4, and 5 put together all three-digit odd numbers. How many are there?
• Sitting 6612
  Seven boys are sitting next to each other in the cinema. How many ways can they sit on the seats if the boys want to sit next to each other?
• Probability 7627
  In the monitored group of people, 8% are ill with the flu. One hundred people from this group were examined. What is the probability that at most 5 of them will be sick with the flu? (round to 3 decimal places)
• Tournament 7975
  Eight players took part in the table tennis tournament. The tournament system allows players to play with each other only once. How many matches will take place in this tournament?

• Probability 17023
  In the draw pole, five numbers out of 35 are drawn. The third prize is paid for three guessed numbers. What is the probability of winning the third prize if we submit a ticket with one of five numbers?
• Six questions test
  There are six questions in the test. There are three answers to each - only one is correct. To take the exam, students must answer at least four questions correctly. Alan didn't learn, so he circled the answers only by guessing. What is the probability th
• Probability 30421
  There are 25 students in the class, 12 of whom are not ready for math. There are five students in the math class. What is the probability of at least 3 being math-ready?
• Three dice
  The player throwing the three dice asked G. Galilei: "Should I bet on the sum of 11 or the sum of 12?" What did Galilei answer him? Hint: write down all three triples of numbers that can be thrown, have a total of 11, have a total of 12, and compare proba
• Probability 37381
  The machine produces one part in 2 minutes. The probability that it is defective is 0.05. What probability will the machine produce exactly ten defective parts per shift (8 hours)?

• Year-on-year 39353
  The company's turnover for the period 2011-2013 increased by 3.7%. From 2013 to 2019, an average year-on-year decrease in turnover of 5% was recorded. What is the total relative change in turnover from 2013 to 2019?

more math problems »