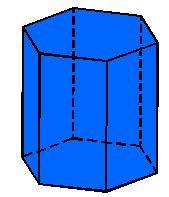
Office
The office building was built in the shape of a regular hexagon inscribed in a circle with a radius of 12 m. The height of the walls is 7m. How much does CZK cost to plaster the building walls per 1 m square cost CZK 400?
Final Answer:
You need to know the following knowledge to solve this word math problem:
solid geometryplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Calculate 25621
 Calculate the area of a regular hexagon inscribed in a circle with a radius r = 7 cm.
Calculate the area of a regular hexagon inscribed in a circle with a radius r = 7 cm. - Inscribed 7018
 The dragon has the shape of a regular hexagon inscribed in a circle with a radius of 20 cm. What is the area of the dragon?
The dragon has the shape of a regular hexagon inscribed in a circle with a radius of 20 cm. What is the area of the dragon? - Hexagon
 Draw a regular hexagon inscribed in a circle with a radius r=15 cm. What is its perimeter?
Draw a regular hexagon inscribed in a circle with a radius r=15 cm. What is its perimeter? - Hexagon A
 Calculate the area of a regular hexagon inscribed in a circle with radius r=15 cm.
Calculate the area of a regular hexagon inscribed in a circle with radius r=15 cm. - Difference 80618
 A regular hexagon is described and inscribed in a circle. The difference between its areas is 8√3. Find the circle's radius.
A regular hexagon is described and inscribed in a circle. The difference between its areas is 8√3. Find the circle's radius. - Circle and hexagon
 Calculate the radius of a circle whose circumference is 8.7 cm longer than the inscribed regular hexagon's circumference.
Calculate the radius of a circle whose circumference is 8.7 cm longer than the inscribed regular hexagon's circumference. - Given is
 Given is the circle x²+y²-4x+2y-11=0. Calculate the area of the regular hexagon inscribed in the given circle.
Given is the circle x²+y²-4x+2y-11=0. Calculate the area of the regular hexagon inscribed in the given circle.
