Biquadratic
By introducing a new variable, solve the biquadratic equation:
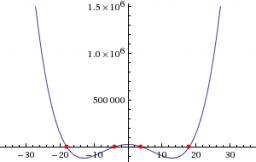
−x4+277x2−15876=0
−x4+277x2−15876=0
Final Answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
algebraarithmeticnumbersGrade of the word problem
Related math problems and questions:
- Equation
 Solve the equation and check the result: 1.6x - 3/2 + x - 9,8 = x + 0,4/3 - 7 + 1,6/6
Solve the equation and check the result: 1.6x - 3/2 + x - 9,8 = x + 0,4/3 - 7 + 1,6/6 - Simple equation 8
 Solve the following equation: 36=-(1+7x)-6(-7-x)
Solve the following equation: 36=-(1+7x)-6(-7-x) - Equation with fraction
 Solve the equation in quotient form: 6x * (3x-2) / x + 7 = 0
Solve the equation in quotient form: 6x * (3x-2) / x + 7 = 0 - Equations
 Solve the following system of equations: 6(x+7)+4(y-5)=12 2(x+y)-3(-2x+4y)=-44
Solve the following system of equations: 6(x+7)+4(y-5)=12 2(x+y)-3(-2x+4y)=-44 - Quadratic - EQ2 - complex
 Solve the quadratic equation: 2y²-8y + 12 = 0
Solve the quadratic equation: 2y²-8y + 12 = 0 - Equation: 6645
 Solve the equation: (2v + 2) / 8 = (v-7) / 4-v
Solve the equation: (2v + 2) / 8 = (v-7) / 4-v - Equation with one variable
 Solve the following equation with one unknown: 5(7s + 5) =130
Solve the following equation with one unknown: 5(7s + 5) =130
