Examples for secondary school students - page 19 of 231
Number of problems found: 4610
- On a mass
 The forces F1, and F2 with magnitudes of 40N act on a mass point M. Their resultant has a magnitude of 60N. Determine the angle that the forces F1 and F2 make.
The forces F1, and F2 with magnitudes of 40N act on a mass point M. Their resultant has a magnitude of 60N. Determine the angle that the forces F1 and F2 make. - Area 51
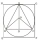 The area of the triangle is 54.39, alpha is 32 °, and gamma is 144 °.
The area of the triangle is 54.39, alpha is 32 °, and gamma is 144 °. - Gardener 5
 The gardener bought 17 apple trees and 11 pears. He paid a total of €111.65. How many euros did 1 pear cost, if we know that its price was 35 cents higher than the price of 1 apple tree? How much would the gardener pay for 28 apple trees and 15 pears?
The gardener bought 17 apple trees and 11 pears. He paid a total of €111.65. How many euros did 1 pear cost, if we know that its price was 35 cents higher than the price of 1 apple tree? How much would the gardener pay for 28 apple trees and 15 pears? - Determine the surface area
 Find the surface area of a cone of height 30 cm whose side makes an angle of 60° with the base plane.
Find the surface area of a cone of height 30 cm whose side makes an angle of 60° with the base plane. - Quadrilateral - irregular
 Find the length of the side d = |AD| in quadrilateral ABCD: a= 35m, b= 120m, c=85m, angle ABC = 105 degrees, angle BCD= 72 degrees
Find the length of the side d = |AD| in quadrilateral ABCD: a= 35m, b= 120m, c=85m, angle ABC = 105 degrees, angle BCD= 72 degrees - Unit circle
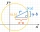 In the Cartesian coordinate system, a unit circle is given on which points A and B lie. Point O is the origin and has coordinates (0,0) and point B has coordinates (1,0). The size of angle BOA is 151°. Determine the x-coordinate of point A.
In the Cartesian coordinate system, a unit circle is given on which points A and B lie. Point O is the origin and has coordinates (0,0) and point B has coordinates (1,0). The size of angle BOA is 151°. Determine the x-coordinate of point A. - X-ray intensity
 The intensity of X-ray radiation is reduced by half when passing through a 13.5 mm thick lead layer. Determine the thickness of the lead plate that will reduce the radiation intensity to one tenth of the original value. If we know that the intensity decre
The intensity of X-ray radiation is reduced by half when passing through a 13.5 mm thick lead layer. Determine the thickness of the lead plate that will reduce the radiation intensity to one tenth of the original value. If we know that the intensity decre - Equation - integers
 Solve the equation with the unknown x from the field of natural numbers 1+6+11+16+. ... +x=970
Solve the equation with the unknown x from the field of natural numbers 1+6+11+16+. ... +x=970 - Rows of chairs
 There are 15 chairs in the first row. There are 3 more chairs in each row. How many chairs are there in the first 20 rows?
There are 15 chairs in the first row. There are 3 more chairs in each row. How many chairs are there in the first 20 rows? - Penny and rolls
 For a hundred crowns I have to buy a hundred pieces of pastry at the prices of rolls of 0.50 crowns, bread 10 crowns, and a roll of 3 crowns. How much of what should I buy? (The Slovak koruna was the currency in Slovakia before the euro or the Czech korun
For a hundred crowns I have to buy a hundred pieces of pastry at the prices of rolls of 0.50 crowns, bread 10 crowns, and a roll of 3 crowns. How much of what should I buy? (The Slovak koruna was the currency in Slovakia before the euro or the Czech korun - In a football
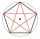 In a football tournament of eight teams, where each team played each other exactly once, points were awarded as follows: the winner of the match received 3 points, the loser received 0 points, and in the event of a draw, each team received 1 point. At the
In a football tournament of eight teams, where each team played each other exactly once, points were awarded as follows: the winner of the match received 3 points, the loser received 0 points, and in the event of a draw, each team received 1 point. At the - Traffic accidents
 Of the total number of traffic accidents, 80% occur in the village and 20% outside the village. If the number of traffic accidents in the village were reduced by 40%, by what percentage would the total number of traffic accidents decrease?
Of the total number of traffic accidents, 80% occur in the village and 20% outside the village. If the number of traffic accidents in the village were reduced by 40%, by what percentage would the total number of traffic accidents decrease? - Instantaneous water heater
 Water flows into and out of an instantaneous water heater at the same time. If water only flows in, the empty water heater would be filled in 18 minutes. If water only flows out, the full water heater would be emptied in 20 minutes. How many hours will it
Water flows into and out of an instantaneous water heater at the same time. If water only flows in, the empty water heater would be filled in 18 minutes. If water only flows out, the full water heater would be emptied in 20 minutes. How many hours will it - Three numbers
 The product of three natural numbers is 600. If we reduced one factor by 10, the product would decrease by 400. If we increased one factor by 5 instead, the product would increase to twice the original value. Which three numbers have this property?
The product of three natural numbers is 600. If we reduced one factor by 10, the product would decrease by 400. If we increased one factor by 5 instead, the product would increase to twice the original value. Which three numbers have this property? - Train - start-up
 A train weighing 1200 tons is supposed to reach a speed of 15 m/s in 45 s when starting up. Determine its acceleration and the magnitude of the force it must exert if the friction force is 0.005 of the train's gravity.
A train weighing 1200 tons is supposed to reach a speed of 15 m/s in 45 s when starting up. Determine its acceleration and the magnitude of the force it must exert if the friction force is 0.005 of the train's gravity. - A car acceleration
 A car increased its speed from 21.6 km/h to 108 km/h on a 54 meter long track. Determine its acceleration, assuming that the motion is uniformly accelerated.
A car increased its speed from 21.6 km/h to 108 km/h on a 54 meter long track. Determine its acceleration, assuming that the motion is uniformly accelerated. - Preparing the mixture
 The seller prepared 25 kg of the mixture for 264 CZK per 1 kg. The first type was 180 CZK per 1 kg and the second was 390 CZK per kg. How much of each did he need?
The seller prepared 25 kg of the mixture for 264 CZK per 1 kg. The first type was 180 CZK per 1 kg and the second was 390 CZK per kg. How much of each did he need? - Green cards
 We draw 4 cards from 32 cards. In how many ways can we draw a) exactly 2 aces, b) 3 green ones
We draw 4 cards from 32 cards. In how many ways can we draw a) exactly 2 aces, b) 3 green ones - In the shipment
 There are 40 products in the shipment. Of these, 4 are defective. In how many ways can we select 5 products so that exactly 3 of them are good?
There are 40 products in the shipment. Of these, 4 are defective. In how many ways can we select 5 products so that exactly 3 of them are good? - Two workshops
 Two workshops were supposed to produce 4000 sets of kitchen utensils together. After completing this task, it was found that the first workshop produced 534 sets more than was originally set for it, while the second workshop fulfilled its task by 80%. How
Two workshops were supposed to produce 4000 sets of kitchen utensils together. After completing this task, it was found that the first workshop produced 534 sets more than was originally set for it, while the second workshop fulfilled its task by 80%. How
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
