Third power - practice problems
Direction: Solve each problem carefully and show your solution in each item.Number of problems found: 168
- Surface = volume
 If the volume and the surface area of a sphere are numerically the same then find its radius.
If the volume and the surface area of a sphere are numerically the same then find its radius. - Three cubes
 Three cubes of iron whose edges are 6 cm, 8 cm, and 10 cm, respectively, are melted and formed into a single cube. Find the edge of the new cube.
Three cubes of iron whose edges are 6 cm, 8 cm, and 10 cm, respectively, are melted and formed into a single cube. Find the edge of the new cube. - Cbrt of fraction
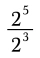 If a fraction is multiplied by itself and then divided by the reciprocal of the same fraction, the result is 18 26/27. Find the fraction.
If a fraction is multiplied by itself and then divided by the reciprocal of the same fraction, the result is 18 26/27. Find the fraction. - Grain storage
 On their farm, Adam's family maintains a storage facility that can hold 19.2 cubic yards (yd3) of grain. Since 1 yard is approximately equal to 0.9144 m, this volume can be converted to m³.
On their farm, Adam's family maintains a storage facility that can hold 19.2 cubic yards (yd3) of grain. Since 1 yard is approximately equal to 0.9144 m, this volume can be converted to m³. - Two numbers 17
 The sum of two numbers is 9, and the sum of their cubes is 189; find the sum of their squares.
The sum of two numbers is 9, and the sum of their cubes is 189; find the sum of their squares. - Vegetable storage
 To help vegetables stay fresh longer, Liam's family maintains storage near their home. The total volume of the root cellar is 737 cubic feet (ft³). Use the fact that 1 foot is approximately equal to 0.3048 m to convert this volume to m³. Round your answer
To help vegetables stay fresh longer, Liam's family maintains storage near their home. The total volume of the root cellar is 737 cubic feet (ft³). Use the fact that 1 foot is approximately equal to 0.3048 m to convert this volume to m³. Round your answer - Perfect square or cube
 Would you classify 324 as a perfect square, perfect cube, both, or neither? ...
Would you classify 324 as a perfect square, perfect cube, both, or neither? ... - A cube 3
 A cube of edge 100 cm has the same volume as a cube of edge 1 m. how many cubic centimeters make 1 cubic meter?
A cube of edge 100 cm has the same volume as a cube of edge 1 m. how many cubic centimeters make 1 cubic meter? - A man 12
 A man in his will shared his money geometrically among his six sons, so the eldest son received ; 5,589 and the youngest son received ; 736. (A)How much will the fourth son receive? (B)How much was shared among them
A man in his will shared his money geometrically among his six sons, so the eldest son received ; 5,589 and the youngest son received ; 736. (A)How much will the fourth son receive? (B)How much was shared among them - Choose 2
 Choose an equivalent expression for three-fourths raised to the fourth power times three-fourths raised to the third power, all raised to the second power.
Choose an equivalent expression for three-fourths raised to the fourth power times three-fourths raised to the third power, all raised to the second power. - Two cubes 3
 Two cubes modeled from plasticine have single-digit integer edge lengths with a difference of 1 cm. Can one large cube with an integer edge length be modeled from the same amount of plasticine?
Two cubes modeled from plasticine have single-digit integer edge lengths with a difference of 1 cm. Can one large cube with an integer edge length be modeled from the same amount of plasticine? - Original model
 When drying, the modeling mass loses 36% of its original volume. If the cube's volume is 5.12 dm³ after drying, what was the original length of the edge?
When drying, the modeling mass loses 36% of its original volume. If the cube's volume is 5.12 dm³ after drying, what was the original length of the edge? - Identical cubes
 What is the volume of a large cube composed of 27 identical small cubes with an edge length of 3 cm?
What is the volume of a large cube composed of 27 identical small cubes with an edge length of 3 cm? - Rectangle and squares
 A 9cm × 15cm rectangle is divided into unit squares. How many paths are there from one rectangle vertex to the opposite vertex if one can only go to the right and up the sides of the squares?
A 9cm × 15cm rectangle is divided into unit squares. How many paths are there from one rectangle vertex to the opposite vertex if one can only go to the right and up the sides of the squares? - Times 81462
 5 to -11 times 5 to -7/5 to zero times 5 to -15 minus ( -5 ) to -2
5 to -11 times 5 to -7/5 to zero times 5 to -15 minus ( -5 ) to -2 - Smallest z9
 Find the smallest positive numbers a and b for which 7a³ = 11b⁵
Find the smallest positive numbers a and b for which 7a³ = 11b⁵ - FINDING GEOMETRIC MEANS
 Find the indicated number of geometric means between the pair of numbers. 16 and 81 [insert 3 members: 16, _, _, _, 81]
Find the indicated number of geometric means between the pair of numbers. 16 and 81 [insert 3 members: 16, _, _, _, 81] - Expressed 79474
 The length of the cube's edge in cm is expressed as a natural number. Its volume is greater than 100 and less than 200. Calculate the surface area of the cube.
The length of the cube's edge in cm is expressed as a natural number. Its volume is greater than 100 and less than 200. Calculate the surface area of the cube. - Smallest 79434
 Find the smallest natural x such that 2x is the square and 3x is the third power of a natural number.
Find the smallest natural x such that 2x is the square and 3x is the third power of a natural number. - Expression with powers
 Which expression is equivalent to 2.1 raised to the fifth power divided by 0.9 raised to the fourth power, all raised to the third power?
Which expression is equivalent to 2.1 raised to the fifth power divided by 0.9 raised to the fourth power, all raised to the third power?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
