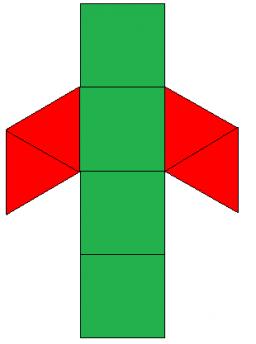
Box
The cardboard is a box-shaped quadrilateral prism with a rhombic base. Rhombus has a side 5 cm, one diagonal 8 cm long, and the box's height is 12 cm. The package will open at the top.
How many cm2 of cardboard do we need to cover overlap and joints that are 5% of the area of cardboard?
Your answer:
How many cm2 of cardboard do we need to cover overlap and joints that are 5% of the area of cardboard?
Your answer:
Tips for related online calculators
Our percentage calculator will help you quickly and easily solve a variety of common percentage-related problems.
Do you want to round the number?
See also our trigonometric triangle calculator.
Do you want to round the number?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
arithmeticsolid geometryplanimetrybasic operations and conceptsGrade of the word problem
Related math problems and questions:
- Cardboard box
We want to make an open-top cardboard box in the shape of a quadrilateral prism with a rhombus-shaped base. The rhombus has a side of 5 cm and one diagonal of 8 cm. The height of the box is 12 cm. How many square centimetres of cardboard are needed if ove - A box 4
A box open at the top has a rectangular base of 200 mm x 300 mm and an altitude of 150 mm. If the base and the sides are 10 mm thick, find the box's total surface area. - Paper box
Calculate the paper consumption on the box-shaped quadrilateral prism with rhombic footstall, base edge a=6 cm, and the adjacent base edges form an angle alpha = 60 °. The box height is 10 cm. How much m² of the paper is consumed 100 such boxes? - Top of the tower
The top of the tower has the shape of a regular hexagonal pyramid. The base edge has a length of 1.2 m. The pyramid height is 1.6 m. How many square meters of sheet metal are needed to cover the top of the tower if 15% extra sheet metal is needed for join - Prism
Calculate the volume of the rhombic prism. The prism base is a rhombus whose one diagonal is 47 cm, and the edge of the base is 27 cm. The edge length and height of the base of the prism are 4:3. - Prism height rhombus
The quadrilateral prism has a volume of 720 cm³. Calculate the height of the prism if the base is a rhombus with a side 16 cm long and a corresponding height of 5 cm. - Prism height calculation
Calculate the height of a regular quadrilateral prism whose base is a rhombus. The edge in the base is 7 cm long, the opposite edges are 5 cm apart, and we also know that the entire body has a volume of 1 dm³.
