Snowman
In a circle with a diameter of 40 cm are drawn three circles (as a snowman) where:
its diameters are integers,
each larger circle diameter is 2 cm larger than the diameter of the previous circle.
Determine the snowman height if we wish for the highest snowman.
its diameters are integers,
each larger circle diameter is 2 cm larger than the diameter of the previous circle.
Determine the snowman height if we wish for the highest snowman.
Final Answer:

Tips for related online calculators
Do you want to round the number?
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetricsbasic operations and conceptsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Snowman 2
 On the medal, which has the shape of a circle with a diameter 39 cm, is sketched a snowman so that the following requirements are met: 1. snowman is composed of three circles, 2. space over the snowman is the same as under it, 3. diameters of all circles
On the medal, which has the shape of a circle with a diameter 39 cm, is sketched a snowman so that the following requirements are met: 1. snowman is composed of three circles, 2. space over the snowman is the same as under it, 3. diameters of all circles - Diameters of circles
 How many percent of the area of a larger circle is a smaller circle if the smaller circle has a diameter of 120 mm and a larger one has a diameter of 300 mm?
How many percent of the area of a larger circle is a smaller circle if the smaller circle has a diameter of 120 mm and a larger one has a diameter of 300 mm? - MO SK/CZ Z9–I–3
 John had the ball that rolled into the pool and swam in the water. Its highest point was 2 cm above the surface. The circle's diameter that marked the water level on the ball's surface was 8 cm. Find the diameter of John's ball.
John had the ball that rolled into the pool and swam in the water. Its highest point was 2 cm above the surface. The circle's diameter that marked the water level on the ball's surface was 8 cm. Find the diameter of John's ball. - Two parallel chords
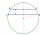 In a circle 70 cm in diameter, two parallel chords are drawn so that the circle's center lies between the chords. Calculate the distance of these chords if one is 42 cm long and the second is 56 cm long.
In a circle 70 cm in diameter, two parallel chords are drawn so that the circle's center lies between the chords. Calculate the distance of these chords if one is 42 cm long and the second is 56 cm long. - Rubberized 19963
 The circular pool with a diameter of 3.5 m is covered with a circular tarpaulin made of rubberized fabric for CZK 110 per square meter. Determine how much the tarpaulin cost if you know that its radius is 25 cm larger than the radius of the pool.
The circular pool with a diameter of 3.5 m is covered with a circular tarpaulin made of rubberized fabric for CZK 110 per square meter. Determine how much the tarpaulin cost if you know that its radius is 25 cm larger than the radius of the pool. - Three figures - numbers
 The sum of three numbers, if each is 10% larger than the previous one, is 662. Determine the figures.
The sum of three numbers, if each is 10% larger than the previous one, is 662. Determine the figures. - Circumference 8395
 The circle's circumference is 321 dm larger than the diameter of the circle. What is the average?
The circle's circumference is 321 dm larger than the diameter of the circle. What is the average?
