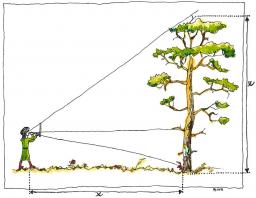
Tree
How tall is the tree observed at the visual angle 45°? If I stand 3 m from the tree, my eyes are two meters above the ground.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Approximately 25381
The observer sees the tops of two trees at the same angle a. It is 9 m from one tree and 21 m from the other. The trees stand on a level. How tall is the second tree if the height of the first is 6 m? Remember that the eyes of a standing person are approx - A radio antenna
Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from - Spruce height
How tall was the spruce that was cut at an altitude of 8m above the ground, and the top landed at a distance of 15m from the heel of the tree? - 45-degree 17861
The ant looks at a 45-degree angle at the top of the tree, 15 m away from the tree. How tall is the tree?
- Broken tree
The tree is broken at 4 meters above the ground. The top of the tree touches the ground at a distance of 5 meters from the trunk. Calculate the original height of the tree. - Clouds
From two points, A and B, on the horizontal plane, a forehead cloud was observed above the two points under elevation angles 73°20' and 64°40'. Points A and B are separated by 2830 m. How high is the cloud? - Opposite 78434
We see the tree on the opposite bank of the river at an angle of 15° from a distance of 41m from the river bank. From the bank of the river, we can see at an angle of 31°. How tall is the tree?
