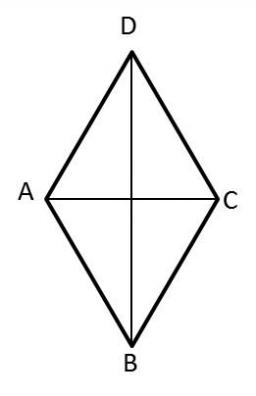
Rhombus
ABCD is a rhombus, ABD is an equilateral triangle, and AC is equal to 4. Find the area of the rhombus.
Final Answer:
Tips for related online calculators
See also our right triangle calculator.
Do you want to convert area units?
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Do you want to convert area units?
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
geometryplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Diagonals of rhombus
Find the length of the diagonal AC of the rhombus ABCD if its perimeter P = 112 dm and the second diagonal BD has a length of 36 dm. - Construction 3357
ABCD rhombus construction entered: a + b = 9 cm; AC = 4.5 cm; height ha = 3.5 cm How long do sides a and b measure? - Construct rhombus
Construct rhombus ABCD if given diagonal length | AC | = 8cm, inscribed circle radius r = 1.5cm - Rhombus
Calculate the length of the diagonal AC of the rhombus ABCD if its perimeter is 524 dm and the other diagonal BD has length 159 dm. - The quadrilateral
The quadrilateral ABCD is composed of two right triangles, ABD and BCD. For side lengths: |AD| = 3cm, | BC | = 12cm, | BD | = 5cm. How many square centimeters (area) does the quadrilateral ABCD have? The angles of DAB and DBC are right. - Calculate square 2556
Calculate the arm length b of the trapezoid ABCD if a = 12 cm, c = 4 cm, the length of AC is same as the length of BC and the area S of the triangle ABC is 9 cm square. - Construct 5333
Construct a rhombus ABCD if AB = 5 cm, BD = 6 cm and AC = 3 cm
